Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang có đáy lớn $BC$ , đáy nhỏ $AD$. Mặt bên $\left( {SAD} \right)$ là tam giác đều, \(\left( \alpha \right)\) là mặt phẳng đi qua $M$ trên cạnh $AB$ , song song với $SA,BC$ . Mp\(\left( \alpha \right)\)cắt các cạnh $CD,SC,SB$ lần lượt tại $N,P,Q.MNPQ$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: d
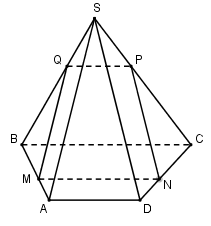
\(\begin{array}{l}\left\{ \begin{array}{l}BC//\left( \alpha \right),BC \subset \left( {ABCD} \right),BC \subset \left( {SBC} \right)\\\left( \alpha \right) \cap \left( {ABCD} \right) = MN\\\left( \alpha \right) \cap \left( {SBC} \right) = PQ\end{array} \right. \Rightarrow MN//BC//PQ\,\,\,\left( 1 \right).\\\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {SAB} \right) = MQ\\\left( \alpha \right)//SA,SA \subset \left( {SAB} \right)\end{array} \right. \Rightarrow SA//MQ.\end{array}\)
Áp dụng định lí Ta-let ta có: \(\dfrac{{AM}}{{AB}} = \dfrac{{SQ}}{{SB}} = \dfrac{{SP}}{{SC}};\dfrac{{AM}}{{AB}} = \dfrac{{DN}}{{DC}} \Rightarrow \dfrac{{SP}}{{SC}} = \dfrac{{DN}}{{DC}} \Rightarrow NP//SD.\)
\(\left\{ \begin{array}{l}MQ//SA\\MN//BC//AD\end{array} \right. \Rightarrow \widehat {NMQ} = \widehat {SAD} = {60^0}.\) (vì tam giác $SAD$ đều)
Tương tự ta chứng ming được \(\widehat {MNP} = \widehat {SDA} = {60^0} \Rightarrow \widehat {NMQ} = \widehat {MNP}\,\,\left( 2 \right).\)
Từ (1) và (2) suy ra $MNPQ$ là hình thang cân.
Hướng dẫn giải:
- Đưa về cùng mặt phẳng.
- Sử dụng các yếu tố song song để xác định hình dạng của thiết diện.
- Dự đoán thiết diện là hình gì?
- Các cách chứng minh một số tứ giác đặc biệt (Hình bình hành, hình thang, hình thang cân, hình thoi,…)
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
