Câu hỏi:
2 năm trước
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a,SA = SB = SC = 2a.{\rm{ }}M$ là một điểm trên đoạn $SB$ mà $SM = m\left( {0 < m < 2a} \right)$. Mặt phẳng \(\left( \alpha \right)\) qua $M$ , song song với $SA,BC$ cắt hình chóp theo thiết diện có chu vi là:
Trả lời bởi giáo viên
Đáp án đúng: b
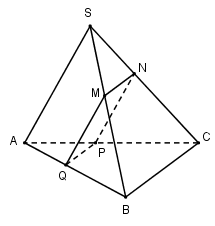
\(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {SAB} \right)\\\left( \alpha \right)//SA \subset \left( {SAB} \right)\end{array} \right. \Rightarrow \) Qua $M$ kẻ \(MQ//SA\left( {Q \in AB} \right) \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = MQ.\)
Tương tự như trên ta xác định được
\(\begin{array}{l}\left( \alpha \right) \cap \left( {ABC} \right) = QP//BC\,\,\left( {P \in AC} \right)\\\left( \alpha \right) \cap \left( {SBC} \right) = MN//BC\,\,\left( {N \in BC} \right)\\\left( \alpha \right) \cap \left( {SAC} \right) = PN//SA\end{array}\)
Suy ra thiết diện của hình chóp khi cắt bởi \(mp\left( \alpha \right)\) là hình bình hành $MNPQ.$
Áp dụng định lý Ta-let ta có:
\(\begin{array}{l}\dfrac{{MN}}{{BC}} = \dfrac{{SM}}{{SB}} \Rightarrow \dfrac{{MN}}{a} = \dfrac{m}{{2a}} \Rightarrow MN = \dfrac{m}{2}\\\dfrac{{QM}}{{SA}} = \dfrac{{BM}}{{BS}} \Rightarrow \dfrac{{QM}}{{2a}} = \dfrac{{2a - m}}{{2a}} \Rightarrow QM = 2a - m.\end{array}\)
Vậy chu vi hình bình hành $MNPQ$ là: \(2\left( {MN + QM} \right) = 2\left( {\dfrac{m}{2} + 2a - m} \right) = m + 4a - 2m = 4a - m.\)
Hướng dẫn giải:
- Đưa về cùng mặt phẳng.
- Xác định thiết diện bằng cách sử dụng yếu tố song song.
- Xác định hình dạng của thiết diện.
- Tính chu vi của thiết diện bằng cách tính tất cả các cạnh của thiết diện dựa vào định lí Ta-let.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
