Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M$ là một điểm trên cạnh $SC$ và \(\left( \alpha  \right)\) là mặt phẳng chứa $AM$ và song song với $BD$. Gọi $E$  và $F$  lần lượt là giao điểm của \(\left( \alpha  \right)\) với các cạnh $SB,SD$ , gọi $I$  là giao điểm của $ME$  và $BC,J$ là giao điểm của $MF$  và $CD$. Nhận xét gì về ba điểm $I,J,A$?

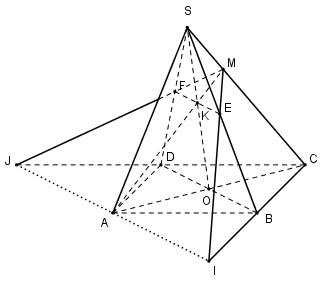
Giả sử dựng được điểm $E,F$ thỏa mãn yêu cầu bài toán.

Ta có: \(\left\{ \begin{array}{l}EF = \left( \alpha  \right) \cap \left( {SBD} \right)\\\left( \alpha  \right)\parallel BD\\BD \subset \left( {SBD} \right)\end{array} \right. \Rightarrow EF\parallel BD.\)

Do đó các điểm $E,F,A,M$  cùng thuộc mặt phẳng \(\left( \alpha  \right)\).

Trong mặt phẳng \(\left( \alpha  \right)\), gọi \(K = EF \cap AM.\)

Ta có: \(K \in EF,EF \subset \left( {SBD} \right) \Rightarrow K \in \left( {SBD} \right).\)

\(K \in AM,AM \subset \left( {SAC} \right) \Rightarrow K \in \left( {SAC} \right) \Rightarrow K \in \left( {SBD} \right) \cap \left( {SAC} \right).\)

Mà \(\left( {SAC} \right) \cap \left( {SBD} \right) = SO\) với \(O = AC \cap BD \Rightarrow K \in SO.\)

Cách dựng $E,F$: Dựng giao điểm $K$  của $AM$  và $SO$ . Qua $K$  kẻ đường thẳng song song với $BD$  cắt $SB$  tại $E$  và cắt $SD$  tại $F$ .

Do \(\begin{array}{l}I = ME \cap BC\\I \in ME,ME \subset \left( \alpha  \right) \Rightarrow I \in \left( \alpha  \right)\\I \in BC,BC \subset \left( {ABCD} \right) \Rightarrow I \in \left( {ABCD} \right).\end{array}\)

Do đó \(I \in \left( \alpha  \right) \cap \left( {ABCD} \right)\)

Tương tự ta cũng có \(J \in \left( \alpha  \right) \cap \left( {ABCD} \right)\)và \(A \in \left( \alpha  \right) \cap \left( {ABCD} \right)\)

Vậy $I,J,A$ cùng thuộc giao tuyến của \(mp\left( \alpha  \right)\) và (ABCD).

Vậy $I,J,A$thẳng hàng.