Cho tứ diện $ABCD$, $G$ là trọng tâm tứ diện. Gọi \({G_1}\) là giao điểm của $AG$ và mặt phẳng $\left( {BCD} \right)$, \({G_2}\) là giao điểm của $BG$ và mặt phẳng $\left( {ACD} \right)$. Khẳng định nào sau đây là đúng?
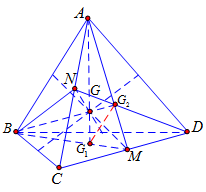
Gọi $M$, $N$ lần lượt là trung điểm của $DC$, $AC$. Vì $G$ là trọng tâm tứ diện nên $G$ là giao điểm của ba đoạn thẳng nối hai trung điểm của cặp cạnh đối của tứ diện như hình vẽ trên.
Xét $\left( {ABM} \right)$: $AG \cap BM = {G_1}$, $BG \cap AM = {G_2}$. Trong $\Delta ACD$ có $AM$ và $DN$ là đường trung tuyến nên \({G_2}\) là trọng tâm của tam giác do đó $\dfrac{{{G_2}M}}{{{G_2}A}} = \dfrac{1}{2}$.
Tương tự ta cũng có $\dfrac{{{G_1}M}}{{{G_1}B}} = \dfrac{1}{2}$ suy ra \({G_1}{G_2}\,{\rm{//}}\,AB\).
Cho lăng trụ đứng tam giác \(ABC.A'B'C'\) có đáy là một tam giác vuông cân tại \(B\), \(AB = BC = a\), \(AA' = a\sqrt 2 \), \(M\) là trung điểm \(BC\). Tính khoảng cách giữa hai đường thẳng\(AM\) và \(B'C\).
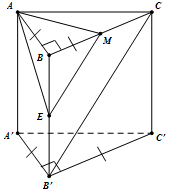
Gọi \(E\) là trung điểm của \(BB'\). Khi đó:$EM{\kern 1pt} \;{\rm{//}}\;B'C$ \( \Rightarrow B'C{\kern 1pt} \;{\rm{//}}\;(AME)\)
Ta có: \(d\left( {AM,B'C} \right) = d\left( {B'C,\left( {AME} \right)} \right) = d\left( {C,\left( {AME} \right)} \right) = d\left( {B,\left( {AME} \right)} \right)\)
Xét khối chóp \(BAME\) có các cạnh \(BE\), \(AB\), \(BM\) đôi một vuông góc với nhau nên
\(\dfrac{1}{{{d^2}\left( {B,\left( {AME} \right)} \right)}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{M{B^2}}} + \dfrac{1}{{E{B^2}}}\)\( \Leftrightarrow \dfrac{1}{{{d^2}\left( {B,\left( {AME} \right)} \right)}} = 7{a^2}\)\( \Leftrightarrow {d^2}\left( {B,\left( {AME} \right)} \right) = \dfrac{{{a^2}}}{7}\)
\( \Leftrightarrow d\left( {B,\left( {AME} \right)} \right) = \dfrac{a}{{\sqrt 7 }}\).
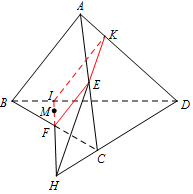
Cho tứ diện \(ABCD\). Gọi \(E\), \(F\) lần lượt là trung điểm của các cạnh \(AC\) và \(BC\). Trên mặt phẳng \(\left( {BCD} \right)\) lấy một điểm \(M\) tùy ý (điểm \(M\) có đánh dấu tròn như hình vẽ). Nêu đầy đủ các trường hợp (TH) để thiết diện tạo bởi mặt phẳng \(\left( {MEF} \right)\) với tứ diện \(ABCD\) là một tứ giác.
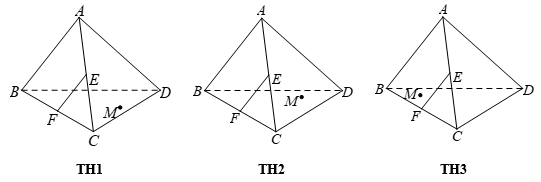
Hình ở TH1: Trong \(\left( {BCD} \right)\): Kẻ \(FM\) cắt \(CD\) tại \(H\). Thiết diện là tam giác \(EFH\).
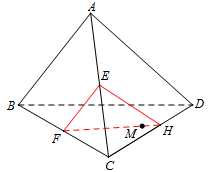
Hình ở TH2:
Trong \(\left( {BCD} \right)\): Kẻ \(FM\) cắt \(BD\) tại \(I\), cắt \(CD\) tại \(H\).
Trong \(\left( {ACD} \right)\): Kẻ \(HE\) cắt \(AD\) tại \(K\).
Thiết diện là tứ giác \(EFIK\).
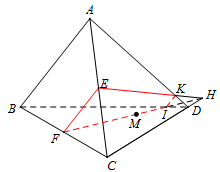
Hình ở TH3:
Trong \(\left( {BCD} \right)\): Kẻ \(FM\) cắt \(BD\) tại \(I\), cắt \(CD\) tại \(H\).
Trong \(\left( {ACD} \right)\): Kẻ \(HE\) cắt \(AD\) tại \(K\).
Thiết diện là tứ giác \(EFIK\).
Cho hình hộp \(ABCD.A'B'C'D'\). Trên các cạnh \(AA'\), \(BB'\), \(CC'\) lần lượt lấy ba điểm \(M\), \(N\), \(P\) sao cho \(\dfrac{{A'M}}{{AA'}} = \dfrac{1}{3}\), \(\dfrac{{B'N}}{{BB'}} = \dfrac{2}{3}\), \(\dfrac{{C'P}}{{CC'}} = \dfrac{1}{2}\). Biết mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(DD'\) tại \(Q\). Tính tỉ số \(\dfrac{{D'Q}}{{DD'}}\).
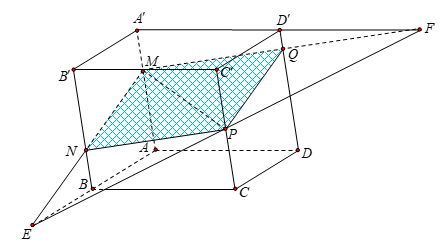
Ta có \(\left\{ \begin{array}{l}\left( {BB'C'C} \right)\,{\rm{//}}\,\left( {AA'D'D} \right)\\\left( {MNP} \right) \cap \left( {BB'C'C} \right) = NP\\\left( {MNP} \right) \cap \left( {AA'D'D} \right) = MQ\end{array} \right. \Rightarrow NP\,{\rm{//}}\,MQ\).
Tương tự: \(\left\{ \begin{array}{l}\left( {AA'B'B} \right)\,{\rm{//}}\,\left( {CC'D'D} \right)\\\left( {MNP} \right) \cap \left( {AA'B'B} \right) = MN\\\left( {MNP} \right) \cap \left( {CC'D'D} \right) = PQ\end{array} \right. \Rightarrow MN\,{\rm{//}}\,PQ\)
Suy ra mặt phẳng \(\left( {MNP} \right)\) cắt hình hộp theo thiết diện là hình bình hành \(MNPQ\).
Mặt khác \(\left\{ \begin{array}{l}BN = \dfrac{1}{3}BB' = \dfrac{1}{3}AA'\\AM = \dfrac{2}{3}AA'\end{array} \right. \Rightarrow \dfrac{{BN}}{{AM}} = \dfrac{1}{2}\).
Trong mặt phẳng \(\left( {ABB'A'} \right)\), gọi \(E\) là giao điểm của hai đường thẳng \(MN\) và \(AB\) thì \(BN\) là đường trung bình của tam giác \(AME\) \( \Rightarrow N\) là trung điểm của đoạn thẳng \(ME\).
Trong mặt phẳng \(\left( {MNPQ} \right)\), gọi \(F\) là giao điểm của \(EP\) và \(MQ\) thì \(NP\) là đường trung bình của tam giác $MEF$ (vì \(NP\,{\rm{//}}\,MQ\) và \(N\) là trung điểm \(EM\)) \( \Rightarrow NP = \dfrac{1}{2}MF\)
Mà tứ giác \(MNPQ\) là hình bình hành nên \(NP = MQ \Rightarrow Q\) là trung điểm \(MF\) hay \(\dfrac{{FQ}}{{FM}} = \dfrac{1}{2}\)
Lại có \(D'Q\,{\rm{//}}\,A'M \Rightarrow \dfrac{{D'Q}}{{A'M}} = \dfrac{{FQ}}{{FM}} = \dfrac{1}{2}\)
\( \Leftrightarrow \dfrac{{D'Q}}{{\dfrac{1}{3}AA'}} = \dfrac{1}{2} \Leftrightarrow \dfrac{{D'Q}}{{DD'}} = \dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6}\)
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(M\) là điểm trên cạnh \(AC\) sao cho \(AC = 3MC\). Lấy \(N\) trên cạnh \(C'D\) sao cho \(C'N = xC'D\). Với giá trị nào của \(x\) thì \(MN\;{\rm{//}}\;BD'\).
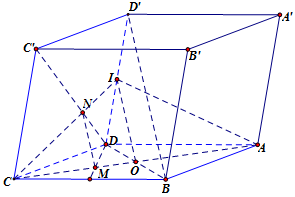
Ta có: \(M\) là điểm trên cạnh \(AC\) sao cho \(AC = 3MC\). Nên \(M\) là trọng tâm của tam giác \(BCD\).
Gọi \(O\) và \(I\) lần lượt là trung điểm của \(AC\) và \(DD'\). Khi đó ta có: \(BD'\;{\rm{//}}\;\left( {IAC} \right)\).
Trong \(\left( {CDD'C'} \right)\), gọi \(N' = CI \cap C'D\). Suy ra \(N'\) là trọng tâm tam giác \(CDD'\).
Do đó: \(\dfrac{{CM}}{{CO}} = \dfrac{2}{3} = \dfrac{{CN'}}{{CI}}\) \( \Rightarrow MN'\;{\rm{//}}\;OI\), mà \(OI\;{\rm{//}}\;BD'\) nên \(MN'\;{\rm{//}}\;BD'\).
Vậy \(N' \equiv N\) và \(x = \dfrac{2}{3}\)

