Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật. Mặt phẳng \(\left( P \right)\) cắt các cạnh \(SA\), \(SB\), \(SC\), \(SD\) lần lượt tại $M$, \(N\), \(P\), \(Q\) . Gọi \(I\) là giao điểm của \(MQ\) và \(NP\). Câu nào sau đây đúng?
Trả lời bởi giáo viên
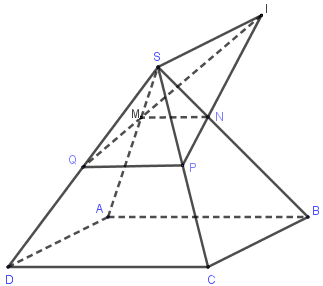
Xét ba mặt phẳng \(\left( {MNPQ} \right),\left( {SAD} \right),\left( {SCB} \right)\) ta có:
\(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {SAD} \right) = MQ\\\left( {MNPQ} \right) \cap \left( {SBC} \right) = NP\\\left( {SAD} \right) \cap \left( {SBC} \right) = d\end{array} \right.\)
Mà \(MQ \cap NP = I\) nên \(d\) đi qua \(I\) hay giao tuyến của \(\left( {SAD} \right),\left( {SBC} \right)\) chính là \(SI\)
Ngoài ra, ta đã biết giao tuyến của \(\left( {SAD} \right),\left( {SBC} \right)\) là đường thẳng đi qua \(S\) và song song với \(AD,BC\)
Vậy \(SI//AD//BC\)
Hướng dẫn giải:
Sử dụng định lý ba giao tuyến để tìm điểm \(I\) rồi từ đó kiểm tra tính đúng sai của từng đáp án.

