Một kim tự tháp Ai Cập được xây dựng khoảng 2500 năm trước công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao ${\rm{150 m}}$, cạnh đáy dài ${\rm{220 m}}$. Hỏi diện tích xung quanh của kim tự tháp đó bằng bao nhiêu?
Trả lời bởi giáo viên
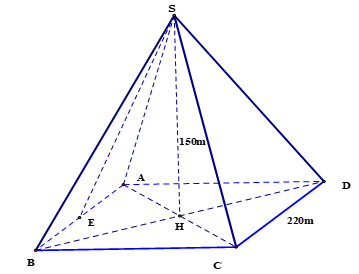
Dễ thấy $BD = \sqrt {B{C^2} + C{D^2}} = 220\sqrt 2 \,\, \Rightarrow BH = \dfrac{1}{2}BD = 110\sqrt 2 $
Trong tam giác vuông $SHB$, có $SB = \sqrt {S{H^2} + B{H^2}} = \sqrt {{{150}^2} + {{\left( {110\sqrt 2 } \right)}^2}} = 10\sqrt {467} $
Vì $S.ABCD$ là hình chóp đều $ \Rightarrow $$SA = SB = SC = SD = 10\sqrt {467} $
Gọi $E$ là trung điểm của $AB$
Trong tam giác vuông $SEA$, có $SE = \sqrt {S{A^2} - E{A^2}} = \sqrt {{{\left( {10\sqrt {467} } \right)}^2} - {{110}^2}} = 10\sqrt {346} $
Vậy ${S_{xq}} = 4{S_{ABC}} = 4.\dfrac{1}{2}SE.AB = 2.10\sqrt {346} .220 = 4400\sqrt {346} \,\left( {{{\rm{m}}^{\rm{2}}}} \right)$
Hướng dẫn giải:
- Diện tích xung quanh của hình chóp là tổng diện tích của các mặt bên.
- Tính độ dài cạnh bên của hình chóp và suy ra diện tích mỗi mặt bên rồi kết luận.

