Cho hình lăng trụ $ABC.A'B'C'$. Gọi $I$, $J$, $K$ lần lượt là trọng tâm của các tam giác $ABC$, $ACC'$, $A'B'C'$. Mặt phẳng nào sau đây song song với mặt phẳng $\left( {IJK} \right)$?
Trả lời bởi giáo viên
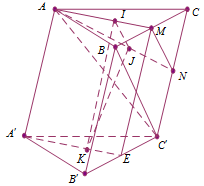
Gọi $M$, $N$, $E$ lần lượt là trung điểm của $BC$, $CC'$, $B'C'$. Suy ra $\dfrac{{AI}}{{IM}} = \dfrac{{AJ}}{{JN}} = 2$ (tính chất trọng tâm tam giác) nên $IJ{\rm{//}}MN$$\left( 1 \right)$.
Trong mặt phẳng $\left( {AA'EM} \right)$ ta có $\dfrac{{AI}}{{IM}} = \dfrac{{A'K}}{{KE}} = 2 \Rightarrow IK{\rm{//}}ME$ mà $ME{\rm{//}}BB'$ nên $IK{\rm{//}}BB'$$\left( 2 \right)$.
Từ $\left( 1 \right)$ và $\left( 2 \right)$ và do $\left( {IJK} \right)$ và $\left( {BB'C'} \right)$ là hai mặt phẳng phân biệt, $IJ,IK \subset \left( {IJK} \right)$ và $MN,BB' \subset \left( {BB'C'} \right)$
=>$\left( {IJK} \right){\rm{//}}\left( {BB'C'} \right)$.
Hướng dẫn giải:
Muốn tìm mặt phẳng song song với \(\left( {IJK} \right)\) ta tìm hai đường thẳng cắt nhau mà song song với hai trong ba đường thẳng nằm trong mặt phẳng \(\left( {IJK} \right)\)
Mặt phẳng chứa hai đường thẳng cắt nhau vừa tìm được ở trên chính là mặt phẳng cần tìm.

