Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Giao tuyến của \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là
Trả lời bởi giáo viên
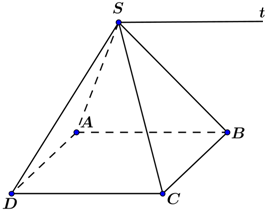
Xét ba mặt phẳng \(\left( {SAB} \right),\left( {SCD} \right),\left( {ABCD} \right)\) ta có:
\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\\left( {SAB} \right) \cap \left( {SCD} \right) = d\end{array} \right.\)
Mà \(AB//CD\) nên \(AB//CD//d\)
Ngoài ra, \(S \in \left( {SAB} \right) \cap \left( {SCD} \right) = d\) nên giao tuyến \(d\) chính là đường thẳng đi qua \(S\) và song song với \(AB,CD\)
Hướng dẫn giải:
Sử dụng định lý giao tuyến của ba mặt phẳng nếu không đồng quy thì song song, từ đó xác định đúng giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\)

