Xét phép quay tâm $O$, góc quay \(\alpha \ne k2\pi ,k \in Z\). Hỏi có bao nhiêu điểm biến thành chính nó qua \(Q\left( {O;\alpha } \right)\) đã cho
Phép quay tâm $O$ góc quay \(\alpha \ne k2\pi ,k \in Z\) biến điểm $O$ thành chính nó.
Trong mặt phẳng $Oxy$ cho hai đường thẳng \(a:\,\,2x + y + 5 = 0\) và \(b:\,\,x - 2y - 3 = 0\). Nếu có một phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc đó có thể là góc nào trong các góc cho dưới đây:
Ta có: \({\overrightarrow n _a} = \left( {2;1} \right),{\overrightarrow n _b} = \left( {1; - 2} \right) \Rightarrow {\overrightarrow n _a}.{\overrightarrow n _b} = 0 \Rightarrow a \bot b\)
Do đó tồn tại phép quay góc \({90^0}\) biến đường thẳng này thành đường thẳng kia
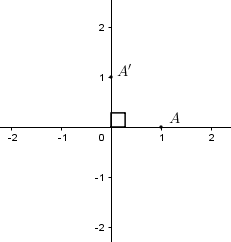
Trong mặt phẳng tọa độ $Oxy$ cho phép quay tâm $O$ biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right)\). Khi đó nó biến điểm \(M\left( {1; - 1} \right)\) thành điểm:
Phép quay tâm $O$ biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right)\) là phép quay tâm $O$ góc \({90^0}\)
Gọi \(M'\left( {x';y'} \right)\) là ảnh của điểm \(M\left( {1; - 1} \right)\) qua phép quay tâm $O$ góc \({90^0}\) ta có: \(\left\{ \begin{array}{l}x' = 1.\cos {90^0} + 1.\sin {90^0}\\y' = 1.\sin {90^0} - 1.\cos {90^0}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x' = 1\\y' = 1\end{array} \right. \Rightarrow M'\left( {1;1} \right)\)
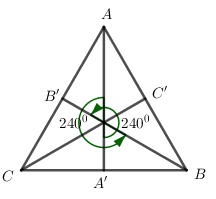
Cho tam giác $ABC$ đều tâm $O$ và các đường cao $AA',BB',CC'$ (các đỉnh của tam giác ghi theo chiều quay của kim đồng hồ). Ảnh của đường cao $AA'$ qua phép quay \(Q\left( {O;{{240}^0}} \right)\) là:
\({Q_{\left( {O;{{240}^0}} \right)}}\left( A \right) = B,{Q_{\left( {O;{{240}^0}} \right)}}\left( {A'} \right) = B' \Rightarrow {Q_{\left( {O;{{240}^0}} \right)}}\left( {AA'} \right) = BB'\)
Gọi $m$ là ảnh của đường thẳng $d$ qua phép quay tâm $I$ góc quay \(\alpha \) (biết rằng $I$ không nằm trên $d$), đường thẳng $d$ song song với $m$ khi:
Ta dễ thấy chỉ có phép quay tâm $I$ góc quay \(\varphi = - \pi \) biến $d$ thành $m$ sao cho $d//m$ .
Chọn câu sai ?
Hiển nhiên A đúng.
\({D_O}\left( A \right) = A' \Rightarrow \left\{ \begin{array}{l}OA = OA'\\\left[ \begin{array}{l}\widehat {AOA'} = {180^0}\\\widehat {AOA'} = - {180^0}\end{array} \right.\end{array} \right. \Rightarrow {D_O} = {Q_{\left( {O;{{180}^0}} \right)}} = {Q_{\left( {O; - {{180}^0}} \right)}} \Rightarrow \) B và D đúng.
Ảnh của hai phép quay tâm $O$ góc quay \({90^0}\) và phép quay tâm $O$ góc quay \( - {90^0}\) đối xứng nhau qua $O$.
Khẳng định nào sau đây đúng về phép quay :
A sai vì thiếu điều kiện \(OM = OM'\)
C sai, phép quay bảo toàn khoảng cách giữa hai điểm bất kì nên phép quay là 1 phép dời hình.
D hiển nhiên sai vì $OM = OM'$
Phép quay tâm $O$ góc \( - {90^0}\) biến đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 4x + 1 = 0\) thành đường tròn có phương trình:
Đường tròn $\left( C \right)$ có tâm \(I\left( {2;0} \right)\) , bán kính \(R = \sqrt {{2^2} + {0^2} - 1} = \sqrt 3 \)
\({Q_{\left( {O; - {{90}^0}} \right)}}\left( I \right) = I'\left( {0; - 2} \right) \Rightarrow {Q_{\left( {O; - {{90}^0}} \right)}}:\,\,\left( C \right)\,\, \mapsto \,\,\left( {C'} \right)\) có tâm \(I'\left( {0; - 2} \right)\) và bán kính \(R' = R = \sqrt 3 \)
Vậy phương trình đường tròn \(\left( {C'} \right)\) là: \({\left( {x - 0} \right)^2} + {\left( {y + 2} \right)^2} = 3 \Leftrightarrow {x^2} + {\left( {y + 2} \right)^2} = 3\)
Cho lục giác đều $ABCDEF$, tâm $O$, các đỉnh được đặt theo thứ tự đó và cùng chiều kim đồng hồ. Thực hiện lần lượt phép quay tâm $O$ góc quay \({60^0}\) và phép tịnh tiến theo vector \(\overrightarrow {OC} \) thì ảnh của tam giác $ABO$ là:

\(\begin{array}{l}\left\{ \begin{array}{l}{Q_{\left( {O;{{60}^0}} \right)}}\left( A \right) = F\\{Q_{\left( {O;{{60}^0}} \right)}}\left( B \right) = A\\{Q_{\left( {O;{{60}^0}} \right)}}\left( O \right) = O\end{array} \right. \Rightarrow {Q_{\left( {O;{{60}^0}} \right)}}\left( {ABO} \right) = FAO\\\left\{ \begin{array}{l}{T_{\overrightarrow {OC} }}\left( F \right) = O\\{T_{\overrightarrow {OC} }}\left( A \right) = B\\{T_{\overrightarrow {OC} }}\left( O \right) = C\end{array} \right. \Rightarrow {T_{\overrightarrow {OC} }}\left( {FAO} \right) = OBC\end{array}\)
\(\Rightarrow \Delta AOB\xrightarrow{{{Q}_{\left( O;{{60}^{0}} \right)}}}\Delta FAO\xrightarrow{{{T}_{\overrightarrow{OC}}}}\Delta OBC\)
Trong mặt phẳng $Oxy$ cho đường thẳng \(d:\,\,x - y + 4 = 0\). Hỏi trong $4$ đường thẳng cho bởi các phương trình sau, đường thẳng nào có thể biến thành $d$ qua phép quay tâm \(I\left( {0;3} \right)\) góc quay \(\pi \) ?
Gọi đường thẳng cần tìm là \(\Delta \), ta có: \({Q_{\left( {I;\pi } \right)}}:\,\,\Delta \,\, \mapsto \,\,d \Rightarrow {Q_{\left( {I; - \pi } \right)}}:\,\,d\,\, \mapsto \,\,\Delta \)
Ta lấy hai điểm bất kì thuộc $d$ và tìm ảnh của hai điểm đó qua phép quay \(Q\left( {I; - \pi } \right)\)
Lấy \(A\left( {0;4} \right);B\left( { - 4;0} \right) \in d\)
Gọi \(A',B'\) lần lượt là ảnh của $A$ và $B$ qua phép quay \(Q\left( {I; - \pi } \right)\)
Ta có: \(\left\{ \begin{array}{l}IA = IA'\\\widehat {AIA'} = - {180^0}\end{array} \right. \Rightarrow \) I là trung điểm của \(AA' \Rightarrow A'\left( {0;2} \right)\)
Tương tự ta có $I$ là trung điểm của \(BB' \Rightarrow B'\left( {4;6} \right)\)
Vậy phương trình đường thẳng \(\Delta \) đi qua $A$ và $B$ là : \(\dfrac{{x - 0}}{{4 - 0}} = \dfrac{{y - 2}}{{6 - 2}} \Leftrightarrow \dfrac{x}{4} = \dfrac{{y - 2}}{4} \Leftrightarrow x - y + 2 = 0\)
Cho đường thẳng \(d:\,\,3x - y + 1 = 0\), đường thẳng nào trong các đường thẳng có phương trình sau là ảnh của $d$ qua phép quay tâm \(O\left( {0;0} \right)\) góc \({90^0}\) ?
\(Q\left( {O;{{90}^0}} \right)\) biến đường thẳng $d$ thành đường thẳng $d'$ và \(d' \bot d\), khi đó phương trình $d'$ có dạng \(x + 3y + c = 0\)
Lấy \(A\left( {0;1} \right) \in d\), gọi $A'$ là ảnh của $A$ qua $Q\left( {O;{{90}^0}} \right) \Rightarrow A'\left( { - 1;0} \right)$ và \(A' \in d' \Rightarrow - 1 + 3.0 + c = 0 \Leftrightarrow c = 1\)
Vậy phương trình đường thẳng $d'$ là \(x + 3y + 1 = 0\).
Trong mặt phẳng $Oxy$ cho đường thẳng \(d:\,\,2x - y + 1 = 0\). Để phép quay tâm $I$ góc quay \(2017\pi \) biến $d$ thành chính nó thì tọa độ của $I$ là:
\({Q_{\left( {I;2017\pi } \right)}} = {Q_{\left( {I;\pi } \right)}}\) là phép đối xứng tâm $I$, do đó để phép đối xứng tâm $I$ biến đường thẳng $d$ thành chính nó thì \(I \in d\), xét bốn đáp án ta thấy chỉ có đáp án D, điểm \(I\left( {0;1} \right) \in d\).
Khẳng định nào sai ?
Phép quay và phép tịnh tiến đều là phép dời hình, do đó các đáp án A, C, D đúng.
Đáp án B sai vì phép quay có góc quay $90^0$ biến đường thẳng thành đường thẳng vuông góc với nó.
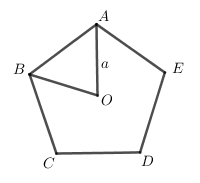
Cho ngũ giác đều $ABCDE$ tâm $O$, biết $OA = a$. Phép quay \({Q_{\left( {C,\pi } \right)}}\) biến $A$ thành $A'$, biến $B$ thành $B'$. Độ dài đoạn $A'B'$ là:
${Q_{\left( {C;\pi } \right)}}\left( A \right) = A',\,\,{Q_{\left( {C;\pi } \right)}}\left( B \right) = B' \Rightarrow {Q_{\left( {C;\pi } \right)}}\left( {AB} \right) = A'B' \Rightarrow A'B' = AB$
Xét tam giác cân $OAB$ có \(\widehat {AOB} = \dfrac{{{{360}^0}}}{5} = {72^0}\)
Áp dụng định lí Cosin ta có :
$\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2.OA.OB.\cos \widehat {AOB}\\\,\,\,\,\,\,\,\,\,\, = {a^2} + {a^2} - 2{a^2}.\cos {72^0} = 2{a^2}\left( {1 - \cos {{72}^0}} \right) = 2{a^2}.2{\sin ^2}{36^0} = 4{a^2}{\sin ^2}{36^0}\\ \Rightarrow AB = 2a\sin {36^0} \Rightarrow A'B' = 2a\sin {36^0}\end{array}$
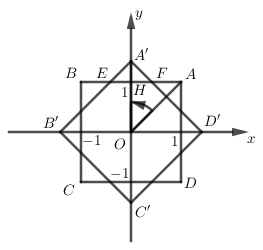
Cho hình vuông $ABCD$ trong đó \(A\left( {1;1} \right),B\left( { - 1;1} \right),C\left( { - 1; - 1} \right),D\left( {1; - 1} \right)\). Xét phép quay \(Q\left( {O;\dfrac{\pi }{4}} \right)\). Giả sử hình vuông $A'B'C'D'$ là ảnh của $ABCD$ qua phép quay đó. Gọi $S$ là diện tích hình vuông $A'B'C'D'$ nằm ngoài hình vuông $ABCD$ . Tính $S$.
\({Q_{\left( {O;\dfrac{\pi }{4}} \right)}}\left( A \right) = A',{Q_{\left( {O;\dfrac{\pi }{4}} \right)}}\left( B \right) = B',{Q_{\left( {O;\dfrac{\pi }{4}} \right)}}\left( C \right) = C',{Q_{\left( {O;\dfrac{\pi }{4}} \right)}}\left( D \right) = D'\) như hình vẽ.
Ta có: \(OA' = OA = \sqrt 2 \Rightarrow A'H = \sqrt 2 - 1\)
Dễ thấy tam giác $A'EF$ là tam giác vuông cân tại $A'$ \( \Rightarrow EF = 2A'H = 2\left( {\sqrt 2 - 1} \right)\)
\( \Rightarrow {S_{\Delta A'EF}} = \dfrac{1}{2}A'H.EF = \dfrac{1}{2}\left( {\sqrt 2 - 1} \right).2\left( {\sqrt 2 - 1} \right) = {\left( {\sqrt 2 - 1} \right)^2}\)
Vậy diện tích hình vuông $A'B'C'D'$ nằm ngoài hình vuông $ABCD$ là \(S = 4{\left( {\sqrt 2 - 1} \right)^2} = 4\left( {3 - 2\sqrt 2 } \right) = 12 - 8\sqrt 2 \)
Cho \({\Delta _1}:2x - y + 1 = 0,\,\;{\Delta _2}:2x - y + 2 = 0,\;{\Delta _3}:y - 1 = 0\)
Phép quay \({Q_{\left( {I,{{180}^o}} \right)}}\) biến \({\Delta _1}\) thành \({\Delta _2}\), biến \({\Delta _3}\) thành chính nó. Tìm tọa độ điểm $I$.
Phép quay \({Q_{\left( {I,{{180}^o}} \right)}}\) biến \({\Delta _3}\) thành chính nó, do đó \(I \in {\Delta _3} \Rightarrow I\left( {a;1} \right)\)
Lấy điểm \(A\left( {0;1} \right) \in {\Delta _1};{Q_{\left( {I;{{180}^0}} \right)}}\left( A \right) = A' \Rightarrow I\) là trung điểm của \(AA' \Rightarrow A'\left( {2a;1} \right)\)
Phép quay \({Q_{\left( {I,{{180}^o}} \right)}}\) là phép đối xứng tâm $I$, biến \({\Delta _1}\,\, \mapsto \,\,{\Delta _2} \Rightarrow A' \in {\Delta _2}\), thay vào ta có:
\(2.2a - 1 + 2 = 0 \Leftrightarrow 4a + 1 = 0 \) \(\Leftrightarrow a = - \dfrac{1}{4}\)
Vậy \(I\left( { - \dfrac{1}{4};1} \right)\)

