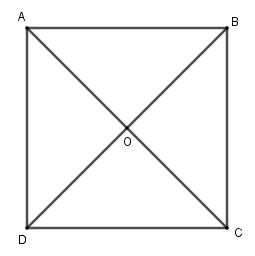
Cho hình vuông tâm $O$. Hỏi có bao nhiêu phép quay tâm $O$, góc quay \(\alpha \,\,\left( {0 < \alpha  \le 360^0} \right)\) biến hình vuông đã cho thành chính nó.

$\begin{array}{l}
{Q_{\left( {O;{{90}^0}} \right)}}\left( A \right) = D\\
{Q_{\left( {O;{{90}^0}} \right)}}\left( B \right) = A\\
{Q_{\left( {O;{{90}^0}} \right)}}\left( C \right) = B\\
{Q_{\left( {O;{{90}^0}} \right)}}\left( D \right) = C\\
\Rightarrow {Q_{\left( {O;{{90}^0}} \right)}}\left( {ABCD} \right) = ABCD\\
{Q_{\left( {O;{{180}^0}} \right)}}\left( A \right) = C\\
{Q_{\left( {O;{{180}^0}} \right)}}\left( B \right) = D\\
{Q_{\left( {O;{{180}^0}} \right)}}\left( C \right) = A\\
{Q_{\left( {O;{{180}^0}} \right)}}\left( D \right) = B\\
\Rightarrow {Q_{\left( {O;{{180}^0}} \right)}}\left( {ABCD} \right) = ABCD\\
{Q_{\left( {O;{{270}^0}} \right)}}\left( A \right) = B\\
{Q_{\left( {O;{{270}^0}} \right)}}\left( B \right) = C\\
{Q_{\left( {O;{{270}^0}} \right)}}\left( C \right) = D\\
{Q_{\left( {O;{{270}^0}} \right)}}\left( D \right) = A\\
\Rightarrow {Q_{\left( {O;{{270}^0}} \right)}}\left( {ABCD} \right) = ABCD\\
{Q_{\left( {O;{{360}^0}} \right)}}\left( A \right) = A\\
{Q_{\left( {O;{{360}^0}} \right)}}\left( B \right) = B\\
{Q_{\left( {O;{{360}^0}} \right)}}\left( C \right) = C\\
{Q_{\left( {O;{{360}^0}} \right)}}\left( D \right) = D\\
\Rightarrow {Q_{\left( {O;{{360}^0}} \right)}}\left( {ABCD} \right) = ABCD
\end{array}$

Vậy có 4 phép quay cần tìm.