Câu hỏi:
2 năm trước
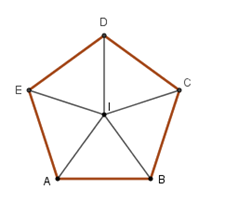
Gọi \(I\) là tâm ngũ giác đều \(ABCDE\) (thứ tự các đỉnh theo chiều dương lượng giác). Kết luận nào sau đây là sai?
Trả lời bởi giáo viên
Đáp án đúng: d
Bước 1:
Vì \(ABCDE\) là ngũ giác đều tâm \(I\) nên \(IA = IB = IC = ID = IE\) và \(\widehat {CID} = \widehat {DIE} = \widehat {EIA} = \widehat {AIB} = \widehat {BIC}\)\( = \dfrac{{360^\circ }}{5} = 72^\circ \)
Bước 2:
Từ đó ta có \({Q_{\left( {I;144^\circ } \right)}}\left( C \right) = E;{Q_{\left( {I;144^\circ } \right)}}\left( D \right) = A\)\( \Rightarrow {Q_{\left( {I;144^\circ } \right)}}\left( {CD} \right) = EA\) nên A đúng
\({Q_{\left( {I;72^\circ } \right)}}\left( A \right) = B;{Q_{\left( {I;72^\circ } \right)}}\left( B \right) = C\)\( \Rightarrow {Q_{\left( {I;72^\circ } \right)}}\left( {AB} \right) = BC\) nên B đúng.
\({Q_{\left( {I;72^\circ } \right)}}\left( A \right) = B;{Q_{\left( {I;72^\circ } \right)}}\left( E \right) = A\)\( \Rightarrow {Q_{\left( {I;72^\circ } \right)}}\left( {AE} \right) = BA\) nên C đúng.
\({Q_{\left( {I;144^\circ } \right)}}\left( B \right) = D;{Q_{\left( {I;144^\circ } \right)}}\left( C \right) = E\)\( \Rightarrow {Q_{\left( {I;144^\circ } \right)}}\left( {BC} \right) = DE\) nên D sai.
Hướng dẫn giải:
Bước 1: Tính số đo các góc \(\widehat {CID};\widehat {DIE};\widehat {EIA};\widehat {AIB};\widehat {BIC}\)
Bước 2: Kiểm tra từng đáp án
Sử dụng phép quay tâm \(I\) góc quay \(\alpha \) biến \(M\) thành \(M'\) thì \(IM = IM'\) và \(\widehat {\left( {IM;IM'} \right)} = \alpha \)
Đáp án A : Tìm ảnh của \(CD\) qua phép quay \({Q_{\left( {I;144^\circ } \right)}}\)
Đáp án B : Tìm ảnh của \(AB\) qua phép quay \({Q_{\left( {I;72^\circ } \right)}}\)
Đáp án C : Tìm ảnh của \(AE\) qua phép quay
Đáp án D : Tìm ảnh của \(BC\) qua phép quay
