Cho hai đường thẳng song song d,d′. Có bao nhiêu phép vị tự tỉ số k=5 biến d thành d′ .
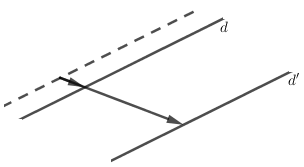
Có vô số phép vị tự tâm không thuộc d với tỉ số k=5 biến đường thẳng d thành d′
Xét phép vị tự V(I,3) biến tam giác ABC thành tam giác A′B′C′. Hỏi chu vi tam giác A′B′C′ gấp mấy lần chu vi tam giác ABC.
Qua phép vị tự V(I,3) thì A′B′=3AB,B′C′=3BC,C′A′=3CA.
Vậy chu vi tam giác A′B′C′ gấp 3 lần chu vi tam giác ABC.
Trong mặt phẳng Oxy cho điểm M(−2;4). Phép vị tự tâm O tỉ số k=−2 biến điểm M thành điểm nào trong các điểm sau?
Gọi điểm M′(x′;y′) là ảnh của điểm M qua phép vị tự tâm O tỉ số k=−2.
V(O;−2)(M)=M′⇔→OM′=−2→OM⇔(x′;y′)=−2(−2;4)⇔{x′=4y′=−8⇒M(4;−8)
Trong mặt phẳng tọa độ Oxy cho phép vị tự V tỉ số k=2 biến điểm A(1;−2) thành điểm A′(−5;1). Hỏi phép vị tự V biến điểm B(0;1) thành điểm có tọa độ nào sau đây?
Gọi B′(x;y) là ảnh của B qua phép vị tự V.
Suy ra →A′B′=(x+5;y−1) và →AB=(−1;3).
Theo giả thiết, ta có →A′B′=2→AB⇔{x+5=2.(−1)y−1=2.3⇔{x=−7y=7.
Trong mặt phẳng tọa độ Oxy cho đường thẳng Δ:x+2y−1=0 và điểm I(1;0). Phép vị tự tâm I tỉ số k biến đường thẳng Δ thành Δ′ có phương trình là:
Để ý thấy I∈Δ do đó phép vị tự tâm I tỉ số k biến đường thẳng Δ thành Δ′ trùng với Δ, với mọi k≠0.
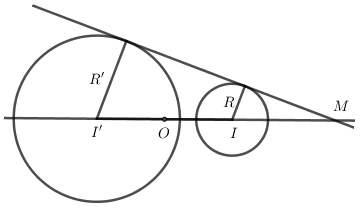
Cho hai tròn ngoài nhau (I;R) và (I′;R′) với R≠R′ . Khẳng định nào sau đây là sai ?
Đáp án A: Gọi M là giao điểm của của đường thẳng nối tâm với tiếp tuyến chung ngoài.
Ta có: {→MI′=→MI.MI′MI=→MI.R′R=k→MIR′=|k|.R
⇒V(M;R′R) biến đường tròn (I;R) thành (I′;R′)
⇒ Đáp án A đúng.
Hiển nhiên đáp án B đúng.
Đáp án C: Giả sử phép vị tự tâm M tỉ số k biến (I;R) thành (I′;R′)⇒|k|=R′R⇒[k=R′Rk=−R′R
⇒ Có hai tâm vị tự biến (I;R) thành (I′;R′)
⇒C đúng.
Đáp án D: Gọi O là trung điểm của II′, giả sử phép vị tự tâm O tỉ số k biến (I;R) thành (I′;R′)
⇒→OI′=k→OI⇒k=−1⇒R′=|−1|R=R(ktm)
⇒ Đáp án D sai.
Phép vị tự tâm I(−1;1) tỉ số k=13 biến đường thẳng d:x−y+4=0 thành đường thẳng có phương trình nào sau đây?
Gọi d′ là ảnh của d qua V(I;13)⇒d′//d⇒ phương trình d′ có dạng x−y+c=0(c≠4)
Lấy điểm A(0;4)∈d , gọi V(I;13)(A)=A′(x′;y′)⇒→IA′=13→IA
⇒(x′+1;y′−1)=13(1;3)⇔{x′+1=13y′−1=1⇒{x′=−23y′=2⇒A′(−23;2)V(I;13)(d)=d′;V(I;13)(A)=A′⇒A′∈d′
Thay tọa độ điểm A′ vào phương trình đường thẳng d′ ta có: −23−2+c=0⇔c=83(tm)
Vậy phương trình đường thẳng d′ là: x−y+83=0⇔3x−3y+8=0
Phép vị tự tâm I(−1;1) tỉ số k=13 biến đường tròn (C):x2+y2=9 thành đường tròn có phương trình nào sau đây?
Đường tròn (C) có tâm K(0;0) bán kính R=3
Gọi K′(x′;y′) là ảnh của điểm K qua phép vị tự V(I;13) ta có :
→IK′=13→IK⇒(x′+1;y′−1)=13(1;−1)⇒{x′+1=13y′−1=−13⇒{x′=−23y′=23⇒K′(−23;23)
Gọi (C′) là ảnh của đường tròn (C) qua phép vị tự V(I;13)⇒ đường tròn (C′) có tâm K′(−23;23) và bán kính R′=|13|.R=1 , do đó (C′) có phương trình (x+23)2+(y−23)2=1.
Cho hai điểm M(−1;4),M′(−4;5). Phép vị tự tỉ số k=2 biến M thành M′ có tâm là điểm nào sau đây?
Gọi tâm vị tự là điểm I(x;y) ta có: V(I;2)(M)=M′⇒→IM′=2→IM
⇒(−4−x;5−y)=2(−1−x;4−y)⇒{−4−x=−2−2x5−y=8−2y⇔{x=2y=3⇒I(2;3)
Phép vị tự nào sau đây biến đường tròn (C):(x−3)2+(y−1)2=4 thành đường tròn (C′):(x−5)2+(y−3)2=4 ?
Đường tròn (C) có tâm K(3;1) và bán kính R=2, đường tròn (C′) có tâm K′(5;3) và bán kính R′=2.
⇒|k|=R′R=1⇒k=±1, mà I′≠I⇒k≠1⇒k=−1
Giả sử phép vị tự tâm I tỉ số k biến K thành K′ ta có: →IK′=−→IK⇒I là trung điểm của KK′⇒I(4;2)
Phép vị tự tỉ số k=2 biến tam giác ABC có số đo các cạnh 3,4,5 thành tam giác A′B′C′ có diện tích là giá trị nào sau đây?
V(I;k)(ΔABC)=ΔA′B′C′⇒ΔA′B′C′∼ΔABC theo tỉ số k⇒SΔA′B′C′SΔABC=k2=4⇒SΔA′B′C′=4SΔABC
Ta có 32+42=52⇒ΔABC là tam giác vuông ⇒SΔABC=12.3.4=6
⇒SΔA′B′C′=4.6=24
Trong mặt phẳng tọa độ Oxy. Cho hai đường thẳng Δ1 và Δ2 lần lượt có phương trình x−2y+1=0 và x−2y+4=0, điểm I(2;1). Phép vị tự tâm I tỉ số k biến đường thẳng Δ1 thành Δ2 khi đó giá trị của k là :
Lấy A(−1;0)∈Δ1, gọi A′(x;y) là ảnh của A qua phép vị tự tâm I tỉ số k ta có : →IA′=k→IA
⇒(x−2;y−1)=k(−3;−1)⇔{x−2=−3ky−1=−k⇒{x=−3k+2y=−k+1⇒A′(−3k+2;−k+1)V(I;k)(Δ1)=Δ2,V(I;k)(A)=A′⇒A′∈Δ2
Thay tọa độ điểm A′ vào phương trình đường thẳng Δ2 ta có:
−3k+2−2(−k+1)+4=0⇔−k+4=0⇔k=4
Trong mặt phẳng tọa độ Oxy cho A(1;2),B(−3;1). Phép vị tự tâm I(2;−1) tỉ số k=2 biến điểm A thành A′ , phép đối xứng tâm B biến A′ thành B′ . Tọa độ điểm B′ là:
V(I;2)(A)=A′(x′;y′)⇒→IA′=2→IA⇒(x′−2;y′+1)=2(−1;3)⇒{x′−2=−2y′+1=6⇔{x′=0y′=5⇒A′(0;5)
B là trung điểm của A′B′ ⇒{x″
Cho đường tròn \left( C \right) có phương trình {\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4 , thực hiện lần lượt phép vị tự tâm O tỉ số k = 2 và phép quay tâm O góc {90^0} biến đường tròn \left( C \right) thành đường tròn nào ?
Đường tròn \left( C \right) có tâm I\left( {2;2} \right) và bán kính R = 2.
Gọi I'\left( {x';y'} \right) = {V_{\left( {O;2} \right)}}\left( I \right) \Rightarrow \overrightarrow {OI'} = 2\overrightarrow {OI} \Rightarrow \left( {x';y'} \right) = 2\left( {2;2} \right) \Rightarrow I'\left( {4;4} \right)
\Rightarrow Ảnh của đường tròn \left( C \right) qua {V_{\left( {O;2} \right)}}\left( I \right) là đường tròn tâm I'\left( {4;4} \right) và bán kính R' = \left| 2 \right|.R = 4
Gọi I''\left( {x'';y''} \right) = {Q_{\left( {O;{{90}^0}} \right)}}\left( {I'} \right) \Rightarrow \left\{ \begin{array}{l}x'' = 4\cos 90 - 4\sin 90 = - 4\\y'' = 4\sin 90 + 4\cos 90 = 4\end{array} \right. \Rightarrow I''\left( { - 4;4} \right)
Phép quay không làm thay đổi bán kính của đường tròn, do đó ảnh của đường tròn \left( {C'} \right) qua phép quay {Q_{\left( {O;{{90}^0}} \right)}} là đường tròn có tâm I''\left( { - 4;4} \right) và bán kính bằng 4, do đó có phương trình: {\left( {x + 4} \right)^2} + {\left( {y - 4} \right)^2} = 16.
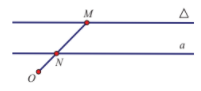
Cho đường thẳng \Delta và điểm O \notin \Delta . Một điểm M thay đổi trên \Delta . Gọi N là trung điểm của đoạn thẳng OM . Khi M thay đổi trên \Delta tập hợp các điểm N là:
Từ giả thiết ta có \overrightarrow {ON} = \dfrac{1}{2}\overrightarrow {OM}
\Rightarrow Phép vị tự tâm O tỉ số k = \dfrac{1}{2} biến điểm M thành điểm N .
Vậy khi M thay đổi trên \Delta thì N thay đổi trên đường a là ảnh của \Delta qua phép vị tự {V_{\left( {O;\dfrac{1}{2}} \right)}} .
\Rightarrow a//\Delta và dễ thấy d\left( {O;a} \right) = \dfrac{1}{2}d\left( {O;\Delta } \right)
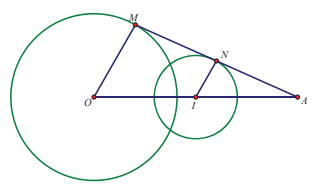
Cho đường tròn \left( {O;R} \right) và một điểm A cố định. Một điểm M thay đổi trên \left( {O;R} \right), gọi N là trung điểm của đoạn thẳng AM . Khi M thay đổi trên \left( {O;R} \right), tập hợp các điểm N là:
Từ giả thiết ta có \overrightarrow {AN} = \dfrac{1}{2}\overrightarrow {AM}
\Rightarrow Phép vị tự {V_{\left( {A;\frac{1}{2}} \right)}}\left( M \right) = N
Vậy khi M thay đổi trên \left( {O;R} \right) thì điểm N thay đổi trên đường tròn \left( T \right) là ảnh của đường tròn \left( {O;R} \right) qua phép vị tự {V_{\left( {A;\frac{1}{2}} \right)}}.
Gọi I là ảnh của O qua {V_{\left( {A;\frac{1}{2}} \right)}} ta có \overrightarrow {AI} = \dfrac{1}{2}\overrightarrow {AO} \Rightarrow I là trung điểm của OA .Vậy \left( T \right) là đường tròn tâm I bán kính \dfrac{R}{2} với I là trung điểm của AO .
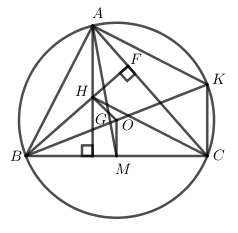
Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O . Phép vị tự tâm G biến H thành O có tỉ số là :
Gọi H và O lần lượt là trực tâm và tam đường tròn ngoại tiếp tâm giác ABC .
Gọi M là trung điểm của BC , kẻ đường kính BK.
Xét đường tròn ngoại tiếp tâm O có \widehat {BCK} nội tiếp chắn nửa đường tròn \Rightarrow \widehat {BCK} = {90^0} \Rightarrow BC \bot CK
Mà AH \bot BC \Rightarrow AH//CK
Tương tự ta chứng minh được AK//CH
\Rightarrow Tứ giác AHCK là hình bình hành \Rightarrow AH = CK
Có OM là đường trung bình của tam giác BCK \Rightarrow OM//CK//AH và OM = \dfrac{1}{2}CK = \dfrac{1}{2}AH.
Gọi G = AM \cap OH ta dễ thấy \Delta AGH \sim \Delta MGO\left( {g.g} \right)
\Rightarrow \dfrac{{AG}}{{MG}} = \dfrac{{AH}}{{OM}} = 2 = \dfrac{{HG}}{{OG}} , mà AM là trung tuyến của tam giác ABC \Rightarrow G là trọng tâm tam giác ABC . Vậy H,G,O thẳng hàng, với G là trọng tâm tam giác ABC và \dfrac{{HG}}{{OG}} = 2 \Rightarrow \overrightarrow {GO} = - \dfrac{1}{2}\overrightarrow {GH}
\Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( H \right) = O.
Cho tam giác ABC. Qua điểm M trên cạnh AB vẽ các đường song song với trung tuyến AE và BF, tương ứng cắt BC và CA tại P,\,\,Q. Tập hợp các điểm R sao cho MPRQ là hình bình hành là:
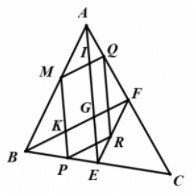
Gọi I = MQ \cap AE,\,\,K = MP \cap BF và G là trọng tâm tam giác ABC.
Ta có:
\begin{array}{l}\frac{{MI}}{{BG}} = \frac{{AM}}{{AB}} = \frac{{AQ}}{{AF}} = \frac{{IQ}}{{GF}}\\ \Rightarrow \frac{{MI}}{{IQ}} = \frac{{BG}}{{GF}} = 2\\ \Rightarrow MI = 2IQ \Rightarrow MI = \frac{2}{3}MQ\\ \Rightarrow \overrightarrow {MI} = \frac{2}{3}\overrightarrow {MQ} \end{array}
Chứng minh tương tự ta có \overrightarrow {MK} = \frac{2}{3}\overrightarrow {MP} .
Vì MIGK là hình bình hành nên ta có:
\begin{array}{l}\overrightarrow {MG} = \overrightarrow {MI} + \overrightarrow {MK} = \frac{2}{3}\overrightarrow {MQ} + \frac{2}{3}\overrightarrow {MP} \\\,\,\,\,\,\,\,\,\,\, = \frac{2}{3}\left( {\overrightarrow {MQ} + \overrightarrow {MP} } \right) = \frac{2}{3}\overrightarrow {MR} \end{array}
(Do MPRQ là hình bình hành).
\Rightarrow \overrightarrow {GR} = - \frac{1}{2}\overrightarrow {GM} \Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( M \right) = R.
Mà M \in AB \Rightarrow R thuộc đường thẳng ảnh của AB qua {V_{\left( {G; - \frac{1}{2}} \right)}}.
Ta có: \left\{ \begin{array}{l}\overrightarrow {GE} = - \frac{1}{2}\overrightarrow {GA} \Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( A \right) = E\\\overrightarrow {GF} = - \frac{1}{2}\overrightarrow {GB} \Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( B \right) = F\end{array} \right. \Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( {AB} \right) = EF.
Vậy khi M di chuyển trên AB thì R di chuyển trên EF.
Cho hình thang ABCD,với \overrightarrow {CD} = - \dfrac{1}{2}\overrightarrow {AB} . Gọi I là giao điểm của hai đường chéo AC và BD. Xét phép vị tự tâm I tỉ số k biến \overrightarrow {AB} thành \overrightarrow {CD} . Mệnh đề nào sau đây là đúng?
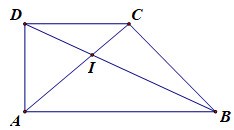
\begin{array}{l}AC \cap BD = \left\{ I \right\}\\{V_{\left( {I;k} \right)}}\left( {AB} \right) = CD\\k\overrightarrow {AB} = \overrightarrow {CD} \Rightarrow k = - \dfrac{1}{2}\end{array}
Cho hình thang ABCD,với \overrightarrow {CD} = - \dfrac{1}{2}\overrightarrow {AB} . Gọi I là giao điểm của hai đường chéo AC và BD. Xét phép vị tự tâm I tỉ số k biến \overrightarrow {AB} thành \overrightarrow {CD} . Mệnh đề nào sau đây là đúng?

\begin{array}{l}AC \cap BD = \left\{ I \right\}\\{V_{\left( {I;k} \right)}}\left( {AB} \right) = CD\\k\overrightarrow {AB} = \overrightarrow {CD} \Rightarrow k = - \dfrac{1}{2}\end{array}

