Cho tam giác \(ABC\). Qua điểm \(M\) trên cạnh \(AB\) vẽ các đường song song với trung tuyến \(AE\) và \(BF\), tương ứng cắt \(BC\) và \(CA\) tại \(P,\,\,Q\). Tập hợp các điểm \(R\) sao cho \(MPRQ\) là hình bình hành là:

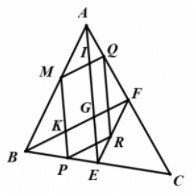
Gọi \(I = MQ \cap AE,\,\,K = MP \cap BF\) và \(G\) là trọng tâm tam giác \(ABC\).

Ta có:

\(\begin{array}{l}\frac{{MI}}{{BG}} = \frac{{AM}}{{AB}} = \frac{{AQ}}{{AF}} = \frac{{IQ}}{{GF}}\\ \Rightarrow \frac{{MI}}{{IQ}} = \frac{{BG}}{{GF}} = 2\\ \Rightarrow MI = 2IQ \Rightarrow MI = \frac{2}{3}MQ\\ \Rightarrow \overrightarrow {MI}  = \frac{2}{3}\overrightarrow {MQ} \end{array}\)

Chứng minh tương tự ta có \(\overrightarrow {MK}  = \frac{2}{3}\overrightarrow {MP} \).

Vì \(MIGK\) là hình bình hành nên ta có:

\(\begin{array}{l}\overrightarrow {MG}  = \overrightarrow {MI}  + \overrightarrow {MK}  = \frac{2}{3}\overrightarrow {MQ}  + \frac{2}{3}\overrightarrow {MP} \\\,\,\,\,\,\,\,\,\,\, = \frac{2}{3}\left( {\overrightarrow {MQ}  + \overrightarrow {MP} } \right) = \frac{2}{3}\overrightarrow {MR} \end{array}\)

(Do \(MPRQ\) là hình bình hành).

\( \Rightarrow \overrightarrow {GR}  =  - \frac{1}{2}\overrightarrow {GM}  \Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( M \right) = R\).

Mà \(M \in AB \Rightarrow R\) thuộc đường thẳng ảnh của \(AB\) qua \({V_{\left( {G; - \frac{1}{2}} \right)}}\).

Ta có: \(\left\{ \begin{array}{l}\overrightarrow {GE}  =  - \frac{1}{2}\overrightarrow {GA}  \Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( A \right) = E\\\overrightarrow {GF}  =  - \frac{1}{2}\overrightarrow {GB}  \Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( B \right) = F\end{array} \right.\) \( \Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( {AB} \right) = EF\).

Vậy khi \(M\) di chuyển trên \(AB\) thì \(R\) di chuyển trên \(EF\).