Câu hỏi:
2 năm trước
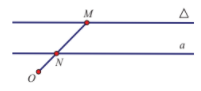
Cho đường thẳng \(\Delta \) và điểm \(O \notin \Delta \). Một điểm $M$ thay đổi trên \(\Delta \). Gọi $N$ là trung điểm của đoạn thẳng $OM$ . Khi $M$ thay đổi trên \(\Delta \) tập hợp các điểm $N$ là:
Trả lời bởi giáo viên
Đáp án đúng: b
Từ giả thiết ta có \(\overrightarrow {ON} = \dfrac{1}{2}\overrightarrow {OM} \)
\( \Rightarrow \) Phép vị tự tâm $O$ tỉ số \(k = \dfrac{1}{2}\) biến điểm $M$ thành điểm $N$ .
Vậy khi $M$ thay đổi trên \(\Delta \) thì $N$ thay đổi trên đường $a$ là ảnh của \(\Delta \) qua phép vị tự \({V_{\left( {O;\dfrac{1}{2}} \right)}}\) .
\( \Rightarrow a//\Delta \) và dễ thấy \(d\left( {O;a} \right) = \dfrac{1}{2}d\left( {O;\Delta } \right)\)
