Câu hỏi:
2 năm trước
Trong mặt phẳng \(\left( P \right)\) cho hình bình hành \(ABCD\). Gọi \(Ax,\,\,By,\,\,Cz,\,\,Dt\) lần lượt là các đường thẳng song song với nhau đi qua \(A,\,\,B,\,\,C,\,\,D\) và nằm về cùng một phía của măt phẳng \(\left( P \right)\) đồng thời không nằm trong \(\left( P \right)\). Một mặt phẳng \(\left( \alpha \right)\) lần lượt cắt \(Ax,\,\,By,\,\,Cz,\,\,Dt\) tại \(A',\,\,B',\,\,C',\,\,D'\) biết \(BB' = 5,2\,\,cm\), \(CC' = 8,6\,\,cm\) , \(DD' = 7,8\,\,cm\). Tính \(AA'\).
Trả lời bởi giáo viên
Đáp án đúng: d
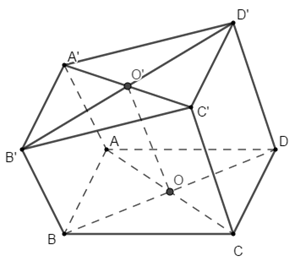
Do \(Ax,\,\,By,\,\,Cz,\,\,Dt\) song song với nhau cắt mặt phẳng \(\left( \alpha \right)\) lần lượt tại \(A',\,\,B',\,\,C',\,\,D'\) nên \(A'B'C'D'\) là hình bình hành và có tâm là \(O'\).
Gọi \(O\) là tâm hình bình hành \(ABCD\).
Ta có \(OO'\) là đường trung bình của hình thang \(BDD'B',\,\,ACC'A'\).
\(\begin{array}{l} \Rightarrow \dfrac{{A'A + CC'}}{2} = O'O = \dfrac{{BB' + D'D}}{2}\\ \Leftrightarrow A'A + CC' = BB' + D'D\\ \Leftrightarrow A'A = 5,2 + 7,8 - 8,6 = 4,4cm\end{array}\)
Hướng dẫn giải:
Dựa vào tính chất đường trung bình của hình thang.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
