Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\). Gọi \(I,\,\,J\) lần lượt là trọng tâm các tam giác \(ABC,\,\,ABD\). Khẳng định nào sau đây đúng ?
Trả lời bởi giáo viên
Đáp án đúng: d
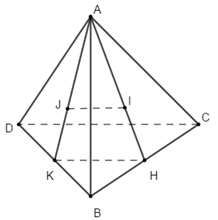
Bước 1:
Gọi \(H,\,\,K\) lần lượt là trung điểm của \(BC,\,\,BD\) \( \Rightarrow HK\parallel CD;HK = \dfrac{1}{2}CD\,\,\,\left( 1 \right)\).
Bước 2:
\(\Delta ABC\) có trọng tâm \(I\), trung tuyến \(AH \Rightarrow \dfrac{{AI}}{{AH}} = \dfrac{2}{3}\).
Tương tự ta có \(\dfrac{{AJ}}{{AK}} = \dfrac{2}{3}\)
Bước 3:
\( \Rightarrow \dfrac{{AI}}{{AH}} = \dfrac{{AJ}}{{AK}} \Rightarrow JI\parallel HK\) (Định lí ta-lét đảo)(2)
=> \(\dfrac{{IJ}}{{HK}} = \dfrac{{AI}}{{AK}} = \dfrac{2}{3} \Rightarrow JI = \dfrac{2}{3}HK\)(3)
Từ (1); (2) và (3) suy ra \(JI\parallel CD;\,\,JI = \dfrac{1}{3}CD\)
Hướng dẫn giải:
Bước 1: Gọi \(H,\,\,K\) lần lượt là trung điểm của \(BC,\,\,BD\) rồi biểu diễn HK theo CD.
Bước 2: Tính \(\dfrac{{AI}}{{AH}}\) và \(\dfrac{{AJ}}{{AK}}\)
Bước 3: Sử dụng định lí ta-lét đảo để chứng minh song song.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
