Cho tứ diện \(ABCD.\) Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AB\) và \(CD.\) Mặt phẳng \(\left( \alpha \right)\) qua \(MN\) cắt \(AD,{\rm{ }}BC\) lần lượt tại \(P\) và \(Q.\) Biết \(MP\) cắt \(NQ\) tại \(I.\) Ba điểm nào sau đây thẳng hàng?
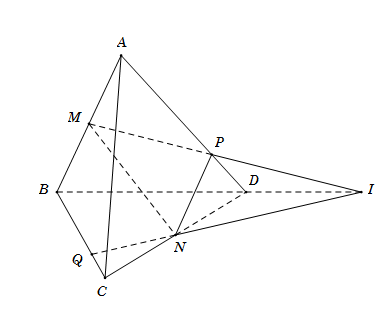
Ta có \(\left( {ABD} \right) \cap \left( {BCD} \right) = BD\).
Lại có \(\left\{ \begin{array}{l}I \in MP \subset \left( {ABD} \right)\\I \in NQ \subset \left( {BCD} \right)\end{array} \right. \Rightarrow I\) thuộc giao tuyến của \(\left( {ABD} \right)\) và \(\left( {BCD} \right)\)
\( \Rightarrow I \in BD \Rightarrow I,{\rm{ }}B,{\rm{ }}D\) thẳng hàng.
Cho tứ diện \(SABC\). Gọi \(L,{\rm{ }}M,{\rm{ }}N\) lần lượt là các điểm trên các cạnh \(SA,{\rm{ }}SB\) và \(AC\) sao cho \(LM\) không song song với \(AB\), \(LN\) không song song với \(SC\). Mặt phẳng \(\left( {LMN} \right)\) cắt các đường thẳng \(AB,{\rm{ }}BC,{\rm{ }}SC\) lần lượt tại \(K,{\rm{ }}I,{\rm{ }}J\). Ba điểm nào sau đây thẳng hàng?
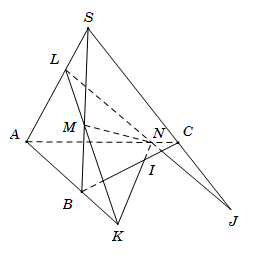
Ta có
● \(M \in SB\) suy \(M\) là điểm chung của \(\left( {LMN} \right)\) và \(\left( {SBC} \right)\).
● \(I\) là điểm chung của \(\left( {LMN} \right)\) và \(\left( {SBC} \right)\).
● \(J\) là điểm chung của \(\left( {LMN} \right)\) và \(\left( {SBC} \right)\).
Vậy \(M,{\rm{ }}I,{\rm{ }}J\) thẳng hàng vì cùng thuộc giao tuyến của \(\left( {LMN} \right)\) và \(\left( {SBC} \right)\).
Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm tam giác \(BCD,\) \(M\) là trung điểm \(CD,\) \(I\) là điểm ở trên đoạn thẳng \(AG,\) \(BI\) cắt mặt phẳng \(\left( {ACD} \right)\) tại \(J.\) Khẳng định nào sau đây sai?
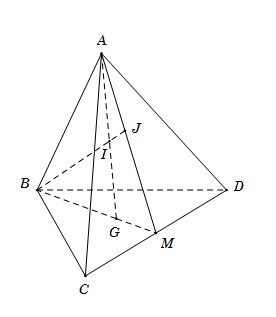
Ta có \(A\) là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)
Do \(BG \cap CD = M \Rightarrow \left\{ \begin{array}{l}M \in BG \subset \left( {ABG} \right) \Rightarrow M \in \left( {ABG} \right)\\M \in CD \subset \left( {ACD} \right) \Rightarrow M \in \left( {ACD} \right)\end{array} \right. \Rightarrow M\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)$\Rightarrow \left( ABG \right)\cap \left( ACD \right)=AM\xrightarrow{{}}$A đúng.
Ta có \(\left\{ \begin{array}{l}BI \subset \left( {ABG} \right)\\AM \subset \left( {ABM} \right)\\\left( {ABG} \right) \equiv \left( {ABM} \right)\end{array} \right. \Rightarrow AM,BI\) đồng phẳng.
\( \Rightarrow J = BI \cap AM \Rightarrow A,J,M\) thẳng hàng$\xrightarrow{{}}$ B đúng.
Ta có $\left\{ \begin{align} & DJ\subset \left( ACD \right) \\ & DJ\subset \left( BDJ \right) \\ \end{align} \right.\Rightarrow DJ=\left( ACD \right)\cap \left( BDJ \right)\xrightarrow{{}}$ D đúng.
Điểm \(I\) di động trên \(AG\) nên \(J\) có thể không phải là trung điểm của \(AM\)
$\xrightarrow{{}}$ C sai
Cho tứ diện \(ABCD\). Gọi \(E,{\rm{ }}F,{\rm{ }}G\) là các điểm lần lượt thuộc các cạnh \(AB,{\rm{ }}AC,{\rm{ }}BD\) sao cho $EF$ cắt \(BC\) tại \(I\), \(EG\) cắt \(AD\) tại \(H\). Ba đường thẳng nào sau đây đồng quy?
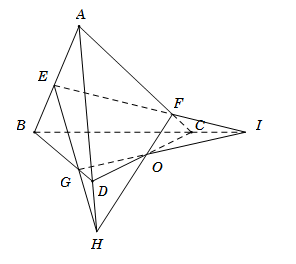
Trong $mp(EHI)$, gọi \(O = HF \cap IG\). Ta có
● \(O \in HF\) mà \(HF \subset \left( {ACD} \right)\) suy ra \(O \in \left( {ACD} \right)\).
● \(O \in IG\) mà \(IG \subset \left( {BCD} \right)\) suy ra \(O \in \left( {BCD} \right)\).
Do đó \(O \in \left( {ACD} \right) \cap \left( {BCD} \right)\). \(\left( 1 \right)\)
Mà \(\left( {ACD} \right) \cap \left( {BCD} \right) = CD\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(O \in CD\).
Vậy ba đường thẳng \(CD,{\rm{ }}IG,{\rm{ }}HF\) đồng quy.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) không phải là hình thang. Trên cạnh \(SC\) lấy điểm \(M\). Gọi \(N\) là giao điểm của đường thẳng \(SD\) với mặt phẳng \(\left( {AMB} \right)\). Mệnh đề nào sau đây đúng?
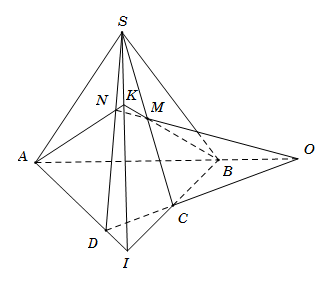
Gọi \(I = AD \cap BC.\) Trong mặt phẳng \(\left( {SBC} \right)\), gọi \(K = BM \cap SI\). Trong mặt phẳng \(\left( {SAD} \right)\), gọi \(N = AK \cap SD\).
Khi đó \(N\) là giao điểm của đường thẳng \(SD\) với mặt phẳng \(\left( {AMB} \right)\).
Gọi \(O = AB \cap CD\). Ta có:
● \(O \in AB\) mà \(AB \subset \left( {AMB} \right)\) suy ra \(O \in \left( {AMB} \right)\).
● \(O \in CD\) mà \(CD \subset \left( {SCD} \right)\) suy ra ${\rm{IJ}},MN,SE$.
Do đó \(O \in \left( {AMB} \right) \cap \left( {SCD} \right)\). \(\left( 1 \right)\)
Mà \(\left( {AMB} \right) \cap \left( {SCD} \right) = MN\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(O \in MN\). Vậy ba đường thẳng $AB,{\rm{ }}CD,{\rm{ }}MN$ đồng quy.
Cho tứ diện $ABCD, M$ là trung điểm của cạnh $CD, G$ là trọng tâm tứ diện. Khi đó $2$ đường thẳng $AD$ và $GM$ là hai đường thẳng:
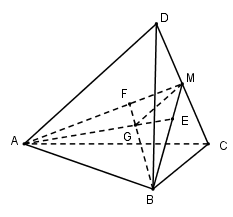
Gọi $M$ là trung điểm của $CD, E$ và $F$ lần lượt là trọng tâm tam giác $BCD$ và $ACD$ \( \Rightarrow E \in BM,F \in AM.\)
Trong $(AMB):$ \(G = AE \cap BF \Rightarrow \) $G$ là trọng tâm của tứ diện $ABCD.$
Giả sử bốn điểm $A, D, G, M$ đồng phẳng.
$A, D, M$ \( \in \left( {ACD} \right) \Rightarrow G \in \left( {ACD} \right) \) \(\Rightarrow AG \subset \left( {ACD} \right) \Rightarrow E \in \left( {ACD} \right)\)(Vô lí)
Do đó $A, D, M, G$ không đồng phẳng.
Vậy $AD$ và $GM$ là hai đường thẳng chéo nhau.
Cho hình chóp \(S.ABCD\) đáy là hình bình hành tâm \(O\). Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SA\), \(SC,\) \(OB\). Gọi \(Q\) là giao điểm của \(SD\) với \(mp\left( {MNP} \right)\). Tính \(\dfrac{{SQ}}{{SD}}.\)
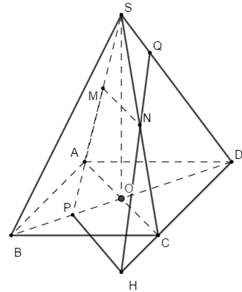
Bước 1:
Trong \(\left( {ABCD} \right)\) lấy \(PH\parallel AC\)\((H \in CD)\)
=> \(PH||MN\) (Do \(AC||MN\))\( \Rightarrow H \in \left( {PMN} \right)\)\( \Rightarrow NH \subset \left( {PMN} \right)\)
Trong \(\left( {SCD} \right)\) gọi \(Q = NH \cap SD\)
Mà \(NH \subset \left( {PMN} \right)\)=> \(Q \in \left( {PMN} \right)\)
Khi đó \(Q\) là giao điểm của \(SD\) với \(mp\left( {MNP} \right)\)
Bước 2:
Mà \(N\) là trung điểm của \(SC \Rightarrow \dfrac{{NC}}{{NS}} = 1\).
Mặt khác áp dụng định lí Ta-lét trong tam giác \(DPH\) ta có \(\dfrac{{HD}}{{HC}} = \dfrac{{DP}}{{OP}} = 3\) (vì \(P\) là trung điểm của \(OB\)).
Bước 3:
Áp dụng định lí Menelaus trong tam giác \(SCD\) với cát tuyến \(QNH\) ta có: \(\dfrac{{HD}}{{HC}}.\dfrac{{NC}}{{NS}}.\dfrac{{QS}}{{QD}} = 1\)
Do đó ta có \(\dfrac{{QS}}{{QD}} = \dfrac{1}{3} \Rightarrow \dfrac{{SQ}}{{SD}} = \dfrac{1}{4}\)

