Câu hỏi:
3 năm trước
Cho tứ diện \(ABCD\). Gọi \(H\), \(K\) lần lượt là trung điểm các cạnh \(AB\), \(BC\). Trên đường thẳng \(CD\) lấy điểm \(M\) nằm ngoài đoạn \(CD\). Thiết diện của tứ diện với mặt phẳng \(\left( {HKM} \right)\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
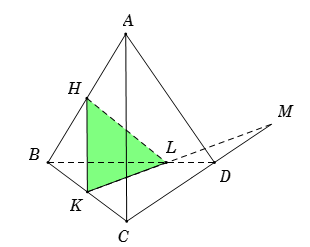
Ta có \(HK\), \(KM\) là đoạn giao tuyến của \(\left( {HKM} \right)\) với \(\left( {ABC} \right)\) và \(\left( {BCD} \right)\).
Trong mặt phẳng \(\left( {BCD} \right)\), do \(KM\) không song song với \(BD\) nên gọi \(L = KM \cap BD\).
Vậy thiết diện là tam giác \(HKL\).
Hướng dẫn giải:
- Tìm các giao tuyến của mặt phẳng \(\left( {HKM} \right)\) với các mặt của tứ diện.
- Từ đó suy ra thiết diện.

