Cho hình chóp $S.ABCD$ , đáy là hình thang, đáy lớn $AB$ , Gọi $O$ là giao của $AC$ với $BD$ . $M$ là trung điểm $SC$ . Giao điểm của đường thẳng $AM$ và $mp\left( {SBD} \right)$ là:
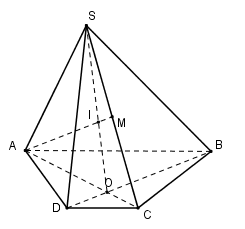
Xét trong $\left( {SAC} \right)$ ta gọi \(I = AM \cap SO,SO \subset \left( {SBD} \right) \) \(\Rightarrow AM \cap \left( {SBD} \right) = I\)
Cho đường thẳng $a$ và mặt phẳng $(P)$ không chứa $a.$ Hai đường thẳng $b$ và $c$ cùng nằm trong mặt phẳng $(P) $ và cùng cắt đường thẳng $a.$ Khả năng nào sau đây không thể xảy ra?
Giả sử đường thẳng $b$ cắt đường thẳng $a$ tại $ M$ thì $M$ là giao điểm của $a$ và $(P)$
Tương tự đường thẳng $c$ cắt $a$ tại $M’$ và $M’$ cũng là giao điểm của $a$ và $(P)$
$⇒ M ≡ M’$( Vì chỉ có duy nhất một giao điểm của đường thẳng a và (P)).
Mà M' thuộc c nên M cũng thuộc c.
$⇒ M$ thuộc b và c
Vậy hai đường thẳng $b$ và $c$ cắt nhau
Cho tứ diện $ABCD. $ Trên cạnh $AB, AC$ lấy các điểm $M, N$ sao cho $MN$ cắt $BC$ tại $E$ và $O$ là điểm bất kì trong tam giác $BCD$ và không nằm trên các cạnh của tam giác $BCD$. Kết luận nào sau đây đúng ?
(I) Giao điểm của $(OMN) $ và $BC $ là điểm $E.$
(II) Giao điểm của $(OMN) $ và $BD$ là giao điểm của $BD$ và $ OE.$
(III) Giao điểm của $(OMN)$ và $CD$ là giao điểm của $CD$ và $ON.$
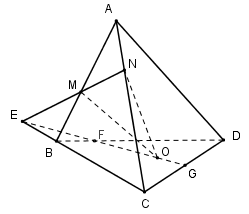
\(E \in BC,E \in MN \subset \left( {OMN} \right) \Rightarrow E = BC \cap \left( {OMN} \right) \) \(\Rightarrow \)(I) đúng.
Trong $(BCD)$ gọi \(F = OE \cap BD \Rightarrow F = BD \cap \left( {OMN} \right) \) \(\Rightarrow \)(II) đúng.
Trong $(BCD)$ gọi \(G = OE \cap CD \Rightarrow G = \left( {OMN} \right) \cap CD \) \(\Rightarrow \) (III) sai.
Gọi $M $ là giao điểm của đường thẳng $a$ và mặt phẳng $(P).$ Khẳng định nào sau đây đúng?
Nếu $M $ là giao điểm của $a$ và $(P):$
Lấy mặt phẳng $(Q)$ bất kỳ chứa $a,$ cắt $(P)$ theo giao tuyến là đường thẳng $d$
$⇒$ Giao điểm của $d$ và $a$ là $M$
Khẳng định A là đúng
Cho hình chóp $S.ABC.$ $M, N$ lần lượt là trung điểm $SA, AB.$ $P$ nằm trên cạnh $BC$ sao cho $BP = 2PC.$ Giao điểm $I$ của $SC$ và $(MNP)$ là:

Có $SC ⊂ (SAC)$
Gọi $Q$ là giao điểm của $NP$ và $AC$
$⇒ (MNP) ∩ (SAC) = MQ$
Gọi $D$ là giao $MQ $ và $SC$
$⇒ D$ là giao của $SC$ và $(MNP)$
Vậy $D \equiv I$ hay $I$ là giao điểm của $MQ$ và $SC$ (với $Q$ là giao điểm của $AC$ với $NP$)
Cho tứ diện \(ABCD\). Gọi \(E,{\rm{ }}F,{\rm{ }}G\) là các điểm lần lượt thuộc các cạnh \(AB,{\rm{ }}AC,{\rm{ }}BD\) sao cho \(EF\) cắt \(BC\) tại \(I\), \(EG\) cắt \(AD\) tại \(H\). Ba đường thẳng nào sau đây đồng quy?
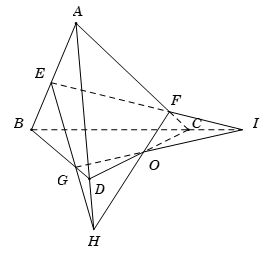
Gọi \(O = HF \cap IG\). Ta có
\(O \in HF\) mà \(HF \subset \left( {ACD} \right)\) suy ra \(O \in \left( {ACD} \right)\).
\(O \in IG\) mà \(IG \subset \left( {BCD} \right)\) suy ra \(O \in \left( {BCD} \right)\).
Do đó \(O \in \left( {ACD} \right) \cap \left( {BCD} \right)\). \(\left( 1 \right)\)
Mà \(\left( {ACD} \right) \cap \left( {BCD} \right) = CD\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(O \in CD\).
Vậy ba đường thẳng \(CD,{\rm{ }}IG,{\rm{ }}HF\) đồng quy.
Cho tứ diện $SABC.$ Trên các cạnh $SA, SB$ và $SC$ lấy các điểm $D, E$ và $F$ sao cho $DE$ cắt $AB$ tại $I, EF$ cắt $BC$ tại $J, FD$ cắt $AC $ tại $K.$ Chọn khẳng định sai?
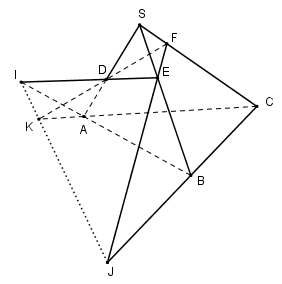
Dễ thấy A và C đúng.
Ta có: \(\left\{ \begin{array}{l}I,J,K \in \left( {DEF} \right)\\I,J,K \in \left( {ABC} \right)\end{array} \right. \) \(\Rightarrow I,J,K \in \left( {DEF} \right) \cap \left( {ABC} \right).\) Mà giao tuyến của hai mặt phẳng là $1$ đường thẳng nên $I, J, K$ cùng thuộc một đường thẳng.
Suy ra $I, J, K$ thẳng hàng. Suy ra B đúng.
Vậy D sai.
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là một tứ giác ($AB$ không song song với $CD$). Gọi $M$ là trung điểm của $SD, N$ là điểm nằm trên cạnh $SB$ sao cho $SN = 2NB,$ $O$ là giao điểm của $AC$ và $BD.$ Giao điểm của $MN$ với $(ABCD) $ là điểm $K.$ Hãy chọn cách xác định điểm $K$ đúng nhất trong bốn phương án sau:
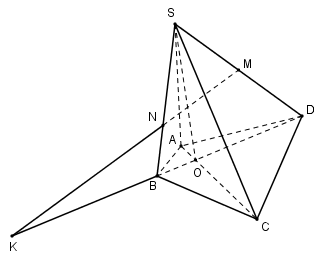
Ta có: \(\dfrac{{SM}}{{SD}} \ne \dfrac{{SN}}{{SB}} \Rightarrow \) $MN$ và $BD$ không song song.
Trong $(SBD) $ gọi \(K = MN \cap BD \Rightarrow K \in BD \subset \left( {ABCD} \right) \Rightarrow K = MN \cap \left( {ABCD} \right).\)
Cho hình bình hành $ABCD$ nằm trong mặt phẳng $(P)$ và một điểm $S$ nằm ngoài mặt phẳng $(P).$ Gọi $M$ là điểm nằm giữa $S$ và $A; N$ là điểm nằm giữa $S$ và $B;$ giao điểm của hai đường thẳng $AC$ và $BD$ là $O;$ giao điểm của hai đường thẳng $CM$ và $SO$ là $I;$ giao điểm của hai đường thẳng $NI$ và $SD$ là $J.$ Tìm giao điểm của $mp(CMN)$ với đường thẳng $SO$ là:
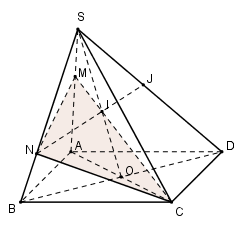
Dễ thấy trong $(SAC)$ có $SO \cap CM = I.$Mà \(CM \subset \left( {CMN} \right) \Rightarrow SO \cap \left( {CMN} \right) = I.\)
Cho tứ diện $ABCD.$ Gọi $M, N$ lần lượt là trung điểm của các cạnh $AD $ và $ BC, G$ là trọng tâm tam giác $BCD.$ Khi đó giao điểm của đường thẳng $MG$ và $mp(ABC)$ là:
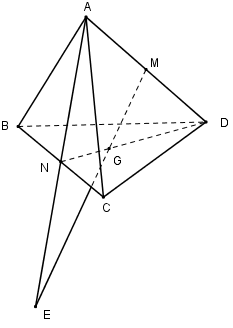
Ta có: \(\dfrac{{DM}}{{DA}} \ne \dfrac{{DG}}{{DN}}\,\,\left( {\dfrac{1}{2} \ne \dfrac{2}{3}} \right) \)
\(\Rightarrow \) $MG$ và $AN$ không song song với nhau.
Trong $(ADN)$ gọi \(E = MG \cap AN.\) Mà \(AN \subset \left( {ABC} \right) \Rightarrow MG \cap \left( {ABC} \right) = E.\)
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\,\,\,\,\left( {a > 0} \right).\) Các điểm \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SA,\,\,SB,\,\,SC\,.\) Mặt phẳng \(\left( {MNP} \right)\) cắt hình chóp theo một thiết diện có diện tích bằng:
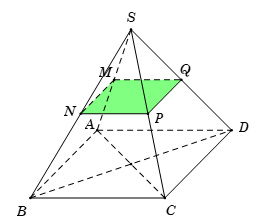
Gọi \(Q\) là trung điểm của \(SD\,.\)
Tam giác \(SAD\) có \(M,\,\,Q\) lần lượt là trung điểm của \(SA,\,\,SD\) suy ra \(MQ\)//\(AD\,.\)
Tam giác \(SBC\) có \(N,\,\,P\) lần lượt là trung điểm của \(SB,\,\,SC\) suy ra \(NP\)//\(BC\,.\)
Mặt khác \(AD//BC\) suy ra \(MQ\)//\(NP\) và \(MQ = NP\,\, \Rightarrow \,\,MNPQ\) là hình vuông.
Khi đó \(M,\,\,N,\,\,P,\,\,Q\) đồng phẳng \( \Rightarrow \,\,\left( {MNP} \right)\) cắt \(SD\) tại \(Q\,\) và \(MNPQ\) là thiết diện của hình chóp \(S.ABCD\) với \(mp\,\,\left( {MNP} \right).\)
Lại có \(\dfrac{{NP}}{{BC}} = \dfrac{1}{2} \Rightarrow \dfrac{{{S_{MNPQ}}}}{{{S_{ABCD}}}} = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4}\).
Vậy diện tích hình vuông \(MNPQ\) là \({S_{MNPQ}} = \dfrac{{{S_{ABCD}}}}{4} = \dfrac{{{a^2}}}{4}.\)
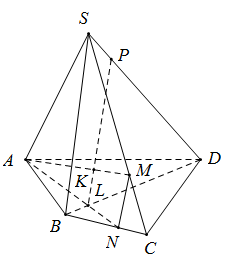
Cho hình chóp $S.ABCD $ có $M, N$ lần lượt nằm trên các cạnh $SC, BC.$ Gọi $P$ là giao điểm của $SD$ với mặt phẳng $(AMN).$ $L$ là giao $AN$ và $BD.$ $K$ là giao $AM$ và $LP.$ Khẳng định nào sau đây đúng?
Vì $L$ là giao của $AN$ và $BD$ nên $L ∈ BD$
$⇒ L ∈ (SBD)$
Có $P ∈ SD ⇒ P ∈ (SBD)$
$ \Rightarrow LP \subset \left( {SBD} \right) \Rightarrow KL \subset \left( {SBD} \right)$
Vì $K ∈ AM; L ∈ AN ⇒ KL ⊂ (AMN)$
Vậy $KL$ là giao tuyến của $(AMN) $ và $(SBD)$
Cho tứ diện \(ABCD\). Gọi \(M,\,N\)lần lượt là trung điểm của các cạnh \(AB\), \(CD\). \(G\)là trung điểm của \(MN\), \(I\)là giao điểm của đường thẳng \(AG\)và mặt phẳng \(\left( {BCD} \right)\). Tính tỉ số \(\dfrac{{GI}}{{GA}}\)?
Trong \(\left( {ABN} \right)\) qua \(M\) kẻ đường thẳng song song với \(AI\) cắt \(BN\) tại \(J\).
Xét tam giác \(MNJ\) ta có: \(\left\{ \begin{array}{l}GI//MJ\\GN = GM\,\left( {gt} \right)\end{array} \right. \Rightarrow GI = \dfrac{1}{2}.MJ\,\,\,\,\left( 1 \right)\)
Xét tam giác \(BAI\) ta có: \(\left\{ \begin{array}{l}MJ//AI\\MA = MB\end{array} \right. \Rightarrow MJ = \dfrac{1}{2}.AI\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\& \left( 2 \right) \Rightarrow GI = \dfrac{1}{4}.AI\)
Mà $AI=GA+IG$
\( \Leftrightarrow \dfrac{{GI}}{{GA}} = \dfrac{1}{3}.\)

