Cho tứ diện $ABCD. $ Trên cạnh $AB, AC$ lấy các điểm $M, N$ sao cho $MN$ cắt $BC$ tại $E$ và $O$ là điểm bất kì trong tam giác $BCD$ và không nằm trên các cạnh của tam giác $BCD$. Kết luận nào sau đây đúng ?
(I) Giao điểm của $(OMN) $ và $BC $ là điểm $E.$
(II) Giao điểm của $(OMN) $ và $BD$ là giao điểm của $BD$ và $ OE.$
(III) Giao điểm của $(OMN)$ và $CD$ là giao điểm của $CD$ và $ON.$
Trả lời bởi giáo viên
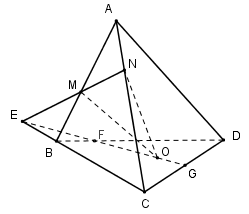
\(E \in BC,E \in MN \subset \left( {OMN} \right) \Rightarrow E = BC \cap \left( {OMN} \right) \) \(\Rightarrow \)(I) đúng.
Trong $(BCD)$ gọi \(F = OE \cap BD \Rightarrow F = BD \cap \left( {OMN} \right) \) \(\Rightarrow \)(II) đúng.
Trong $(BCD)$ gọi \(G = OE \cap CD \Rightarrow G = \left( {OMN} \right) \cap CD \) \(\Rightarrow \) (III) sai.
Hướng dẫn giải:
Suy luận từng đáp án dựa vào giao điểm của đường thẳng và mặt phẳng.

