Câu hỏi:
3 năm trước
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\,\,\,\,\left( {a > 0} \right).\) Các điểm \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SA,\,\,SB,\,\,SC\,.\) Mặt phẳng \(\left( {MNP} \right)\) cắt hình chóp theo một thiết diện có diện tích bằng:
Trả lời bởi giáo viên
Đáp án đúng: c
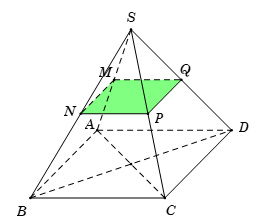
Gọi \(Q\) là trung điểm của \(SD\,.\)
Tam giác \(SAD\) có \(M,\,\,Q\) lần lượt là trung điểm của \(SA,\,\,SD\) suy ra \(MQ\)//\(AD\,.\)
Tam giác \(SBC\) có \(N,\,\,P\) lần lượt là trung điểm của \(SB,\,\,SC\) suy ra \(NP\)//\(BC\,.\)
Mặt khác \(AD//BC\) suy ra \(MQ\)//\(NP\) và \(MQ = NP\,\, \Rightarrow \,\,MNPQ\) là hình vuông.
Khi đó \(M,\,\,N,\,\,P,\,\,Q\) đồng phẳng \( \Rightarrow \,\,\left( {MNP} \right)\) cắt \(SD\) tại \(Q\,\) và \(MNPQ\) là thiết diện của hình chóp \(S.ABCD\) với \(mp\,\,\left( {MNP} \right).\)
Lại có \(\dfrac{{NP}}{{BC}} = \dfrac{1}{2} \Rightarrow \dfrac{{{S_{MNPQ}}}}{{{S_{ABCD}}}} = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4}\).
Vậy diện tích hình vuông \(MNPQ\) là \({S_{MNPQ}} = \dfrac{{{S_{ABCD}}}}{4} = \dfrac{{{a^2}}}{4}.\)
Hướng dẫn giải:
- Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng \(\left( {MNP} \right)\).
- Nhận dạng thiết diện và tính diện tích.
Câu hỏi khác
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
