Câu hỏi:
2 năm trước
Cho tứ diện đều $ABCD$ có cạnh bằng $a\,.$ Gọi $G$ là trọng tâm tam giác $ABC.$ Mặt phẳng $\left( {GCD} \right)$ cắt tứ diện theo một thiết diện có diện tích là:
Trả lời bởi giáo viên
Đáp án đúng: b
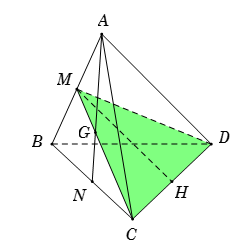
Gọi $M,\,\,N$ lần lượt là trung điểm của $AB,\,\,BC$ suy ra $AN \cap MC = G.$
Dễ thấy mặt phẳng $\left( {GCD} \right)$ cắt đường thắng $AB$ tại điểm $M.$
Suy ra tam giác $MCD$ là thiết diện của mặt phẳng $\left( {GCD} \right)$ và tứ diện $ABCD\,.$
Tam giác $ABD$ đều, có $M$ là trung điểm $AB$ suy ra $MD = \dfrac{{a\sqrt 3 }}{2}.$
Tam giác $ABC$đều, có $M$ là trung điểm $AB$ suy ra $MC = \dfrac{{a\sqrt 3 }}{2}.$
Gọi $H$ là trung điểm của $CD\,\, \Rightarrow \,\,MH \bot CD\,\, \Rightarrow \,\,{S_{\Delta MCD}} = \dfrac{1}{2}.MH.CD$
Với $MH = \sqrt {M{C^2} - H{C^2}} = \sqrt {M{C^2} - \dfrac{{C{D^2}}}{4}} = \dfrac{{a\sqrt 2 }}{2}.$
Vậy ${S_{\Delta MCD}} = \dfrac{1}{2}.\dfrac{{a\sqrt 2 }}{2}.a = \dfrac{{{a^2}\sqrt 2 }}{4}\,.$
Hướng dẫn giải:
- Xác định thiết diện của hình chóp khi cắt bởi \(mp\left( {GCD} \right)\).
- Nhận dạng thiết diện và tính diện tích.
Câu hỏi khác
- Bài tập đường thẳng song song với mặt phẳng toán 11 có lời giải
- Bài tập các bài toán tìm giao điểm của đường thẳng và mặt phẳng toán 11 có lời giải
- Bài tập thiết diện của hình chóp toán 11 có lời giải
- Bài tập hai đường thẳng song song toán 11 có lời giải
- Bài tập đại cương về đường thẳng và mặt phẳng toán 11 có lời giải
