Câu hỏi:
3 năm trước
Cho tứ diện $ABCD.$ Gọi $E$ và $F$ lần lượt là trung điểm của $AB$ và $CD$; $G$ là trọng tâm tam giác $BCD.$ Giao điểm của đường thẳng $EG$ và mặt phẳng $\left( {ACD} \right)$ là
Trả lời bởi giáo viên
Đáp án đúng: b
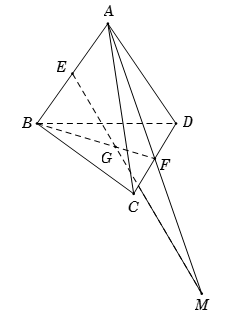
Vì $G$ là trọng tâm tam giác $BCD,\,\,\,F$ là trung điểm của $CD$$ \Rightarrow \,\,\,G \in \left( {ABF} \right)\,.$
Ta có $E$ là trung điểm của $AB$$ \Rightarrow \,\,\,E \in \left( {ABF} \right)\,.$
Trong \(\left( {ABF} \right)\), gọi $M$ là giao điểm của $EG$ và $AF$ mà $AF \subset \left( {ACD} \right)$ suy ra $M \in \left( {ACD} \right)\,.$
Vậy giao điểm của $EG$ và $mp\,\,\left( {ACD} \right)$ là giao điểm $M = EG \cap AF\,.$
Hướng dẫn giải:
Tìm một đường thẳng thuộc mặt phẳng này mà cắt đường thẳng kia, từ đó suy ra giao điểm cần tìm.

