Cho tứ giác \(ABCD\) có \(AC\) và \(BD\) giao nhau tại \(O\) và một điểm \(S\) không thuộc mặt phẳng \(\left( {ABCD} \right)\). Trên đoạn \(SC\) lấy một điểm \(M\) không trùng với \(S\) và \(C\). Giao điểm của đường thẳng \(SD\) với mặt phẳng \(\left( {ABM} \right)\) là
Trả lời bởi giáo viên
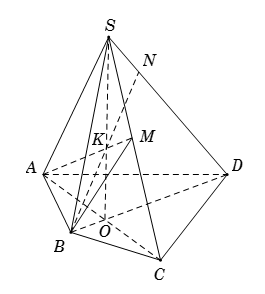
Chọn mặt phẳng phụ \(\left( {SBD} \right)\) chứa \(SD\).
Tìm giao tuyến của hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {ABM} \right)\).
Ta có \(B\) là điểm chung thứ nhất của \(\left( {SBD} \right)\) và \(\left( {ABM} \right)\).
Trong mặt phẳng \(\left( {ABCD} \right)\), gọi \(O = AC \cap BD\). Trong mặt phẳng \(\left( {SAC} \right)\), gọi \(K = AM \cap SO\). Ta có:
▪ \(K \in SO\) mà \(SO \subset \left( {SBD} \right)\) suy ra \(K \in \left( {SBD} \right)\).
▪ \(K \in AM\) mà \(AM \subset \left( {ABM} \right)\) suy ra \(K \in \left( {ABM} \right)\).
Suy ra \(K\) là điểm chung thứ hai của \(\left( {SBD} \right)\) và \(\left( {ABM} \right)\).
Do đó \(\left( {SBD} \right) \cap \left( {ABM} \right) = BK\).
- Trong mặt phẳng \(\left( {SBD} \right)\), gọi \(N = SD \cap BK\). Ta có:
▪ \(N \in BK\) mà \(BK \subset \left( {ABM} \right)\) suy ra \(N \in \left( {ABM} \right)\).
▪ \(N \in SD\).
Vậy \(N = SD \cap \left( {ABM} \right)\).
Hướng dẫn giải:
- Tìm giao tuyến của hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {ABM} \right)\).
- Tìm giao điểm của đường thẳng \(SD\) với giao tuyến vừa tìm được.

