Câu hỏi:
2 năm trước
Cho tứ diện $ABCD$ có $M,N$ lần lượt là trung điểm $AC,BC$. $K$ là điểm thuộc cạnh $BD$ sao cho $BK = 2KD$. Gọi $I$ là giao điểm của $AD$ và $\left( {MNK} \right).$ $MI$ cắt $CD$ tại điểm $E$. Khẳng định nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: c
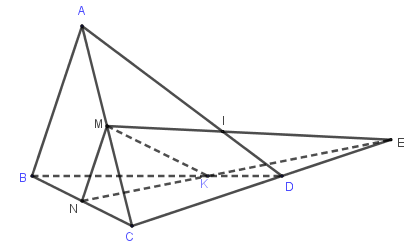
Vì $I$ là giao của $AD$ và $\left( {MNK} \right)$ nên $I \in \left( {MNK} \right)$
$ \Rightarrow MI \subset \left( {MNK} \right)$
Mà $E \in MI \Rightarrow E \in \left( {MNK} \right)$
$ \Rightarrow E$ thuộc giao tuyến của $\left( {MNK} \right)$ và $\left( {BCD} \right)$
$ \Rightarrow E \in NK$
Hướng dẫn giải:
Ta tìm giao tuyến của đường thẳng b và mặt phẳng (α):
+ Tìm một mặt phẳng chứa b thích hợp
+ Tìm giao tuyến của mặt phẳng này với mặt phẳng (α)
+ Tìm giao điểm của giao tuyến đó với đường thẳng b

