Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M$ là trung điểm của $SC.$ Gọi $I$ là giao điểm của $AM$ với mặt phẳng $\left( {SBD} \right).$ Mệnh đề nào dưới đây đúng?
Trả lời bởi giáo viên
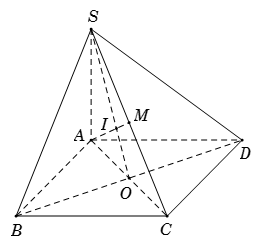
Gọi $O$ là tâm hình bình hành $ABCD$ suy ra $O$ là trung điểm của $AC\,.$
Nối $AM$ cắt $SO$ tại $I$ mà $SO \subset \left( {SBD} \right)$ suy ra $I = AM \cap \left( {SBD} \right).$
Tam giác $SAC$ có $M,\,\,O$ lần lượt là trung điểm của $SC,\,\,AC.$
Mà $I = AM \cap SO$ suy ra $I$ là trọng tâm tam giác $SAC\,\, \Rightarrow \,\,AI = \dfrac{2}{3}AM\,\, \Leftrightarrow \,\,IA = 2IM.$
Điểm $I$ nằm giữa $A$ và $M$ suy ra $\overrightarrow {IA} = 2\overrightarrow {MI} = - \,2\overrightarrow {IM} .$
Hướng dẫn giải:
- Tìm một đường thẳng nằm trong mặt phẳng này và cắt đường thẳng kia, từ đó suy ra giao điểm.
- Sử dụng các mối quan hệ hình học suy ra tính chất của giao điểm.

