Cho hình chóp S.ABC có đáy ABC là tam giác cân, AB = a, $\widehat {BAC} = {120^0}$. Gọi I là trung điểm cạnh AB. Hình chiếu vuông góc của đỉnh S lên mặt phẳng đáy là trung điểm H của CI, góc giữa đường thẳng SA và mặt đáy bằng 600. Tính khoảng cách từ A đến mặt phẳng (SBC).

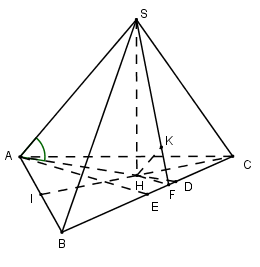
Do $\widehat {BAC} = {120^0}$ nên \(\Delta ABC\) cân tại A.

Xét tam giác ACI có \(CI = \sqrt {A{C^2} + A{I^2} - 2AC.AI.\cos {{120}^0}}  = \dfrac{{a\sqrt 7 }}{2}\)

\( \Rightarrow AH = \sqrt {\dfrac{{A{C^2} + A{I^2}}}{2} - \dfrac{{C{I^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{4}\)

Ta có \(AH \bot \left( {ABC} \right) \Rightarrow \) HA là hình chiếu của SA trên (ABC)

\( \Rightarrow \widehat {\left( {SA;\left( {ABC} \right)} \right)} = \widehat {\left( {SA;HA} \right)} = \widehat {SAH} = {60^0}\)

Xét tam giác vuông SAH : \(SH = AH.\tan 60 = \dfrac{{3a}}{4}\) 

Trong (ABC) kẻ \(AE \bot BC,HF \bot BC\,\,\left( {E;F \in BC} \right)\), \(D = AH \cap \left( {SBC} \right)\).

\( \Rightarrow EH\) là đường trung bình của tam giác BCI \( \Rightarrow EH = \dfrac{1}{2}BI = \dfrac{1}{4}AB = \dfrac{a}{4}\)

Ta có \(AE = AB.\sin 30 = \dfrac{a}{2}\)

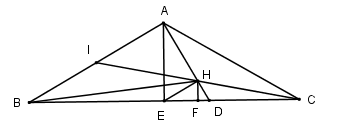
Xét tam giác AEH có : \(A{H^2} + H{E^2} = \dfrac{{{a^2}}}{4} = A{E^2} \Rightarrow \Delta AEH\) vuông tại H (Định lí Py – ta – go đảo) \( \Rightarrow AD = \dfrac{{A{E^2}}}{{AH}} = \dfrac{{a\sqrt 3 }}{3};HD = \dfrac{{E{H^2}}}{{AH}} = \dfrac{{a\sqrt 3 }}{{12}}\)

Ta có: \(AH \cap \left( {SBC} \right) = D \Rightarrow \dfrac{{d\left( {A;\left( {SBC} \right)} \right)}}{{d\left( {H;\left( {SBC} \right)} \right)}} = \dfrac{{AD}}{{HD}} = \dfrac{{\dfrac{{a\sqrt 3 }}{3}}}{{\dfrac{{a\sqrt 3 }}{{12}}}} = 4 \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = 4d\left( {H;\left( {SBC} \right)} \right)\)

Trong (SHF) kẻ \(HK \bot SF\) ta có                                                                                        

\(\begin{array}{l}\left\{ \begin{array}{l}SH \bot BC\\HF \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SHF} \right) \Rightarrow BC \bot HK\\\left\{ \begin{array}{l}HK \bot BC\\HK \bot SF\end{array} \right. \Rightarrow HK \bot \left( {SBC} \right) \Rightarrow d\left( {H;\left( {SBC} \right)} \right) = HK\end{array}\) 

Ta có : \(\dfrac{{HF}}{{AE}} = \dfrac{{HD}}{{AD}} \Rightarrow HF = \dfrac{{AE.HD}}{{AD}} = \dfrac{{\dfrac{a}{2}.\dfrac{{a\sqrt 3 }}{{12}}}}{{\dfrac{{a\sqrt 3 }}{3}}} = \dfrac{a}{8}\)

\( \Rightarrow HK = \sqrt {\dfrac{{S{H^2}.H{F^2}}}{{S{H^2} + H{F^2}}}}  = \sqrt {\dfrac{{{{\left( {\dfrac{{3a}}{4}} \right)}^2}.{{\left( {\dfrac{a}{8}} \right)}^2}}}{{{{\left( {\dfrac{{3a}}{4}} \right)}^2} + {{\left( {\dfrac{a}{8}} \right)}^2}}}}  = \dfrac{{3a}}{{4\sqrt {37} }} \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = 4HK = \dfrac{{3a}}{{\sqrt {37} }} = \dfrac{{3a\sqrt {37} }}{{37}}\)