Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\) có $AC = AD = BC = BD = a$ và hai mặt phẳng $\left( {ACD} \right)$, $\left( {BCD} \right)$ vuông góc với nhau. Tính độ dài cạnh \(CD\) sao cho hai mặt phẳng $\left( {ABC} \right)$, $\left( {ABD} \right)$ vuông góc.
Trả lời bởi giáo viên
Đáp án đúng: a
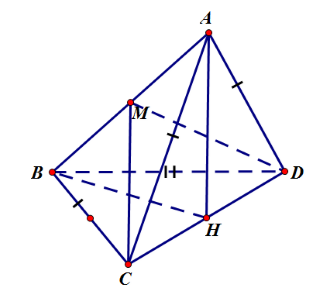
Gọi \(H\) là trung điểm của $CD$ nên \(AH \bot CD\)
\( \Leftrightarrow AH \bot \left( {BCD} \right)\) (do \(\left( {ACD} \right) \bot \left( {BCD} \right)\)) và \(\left( {ACD} \right) \cap \left( {BCD} \right) = CD\)
Gọi \(M\) là trung điểm của $AB$ nên \(CM \bot AB\)
Vì \(\left( {ABC} \right) \bot \left( {ABD} \right)\) và \(\left( {ABC} \right) \cap \left( {ABD} \right) = AB\) \( \Rightarrow CM \bot MD.\)
\(\Delta ABC = \Delta ABD\)\( \Rightarrow MC = MD\)\( \Rightarrow \Delta MCD\) vuông cân tại \(M\).
Đặt \(CD = x\) \( \Rightarrow A{H^2} = B{H^2} = {a^2} + \dfrac{{{x^2}}}{4} \Leftrightarrow A{B^2} = A{H^2} + B{H^2} = 2{a^2} + \dfrac{{{x^2}}}{2}\)
Ta có \(MH = \dfrac{1}{2}AB = \dfrac{1}{2}\sqrt {2{a^2} + \dfrac{{{x^2}}}{2}} \Leftrightarrow MH = \dfrac{{\sqrt 2 }}{2}CD \Leftrightarrow \sqrt {2{a^2} + \dfrac{{{x^2}}}{2}} .\dfrac{1}{2} = \dfrac{{\sqrt 2 }}{2}x\)
\( \Leftrightarrow 2{a^2} + \dfrac{{{x^2}}}{2} = 2{x^2} \Leftrightarrow 4{a^2} = 3{x^2} \Leftrightarrow x = \dfrac{{2a}}{{\sqrt 3 }}\).
Hướng dẫn giải:
- Gọi \(H\) là trung điểm của $CD$, từ điều kiện hai mặt phẳng vuông góc suy ra các mối quan hệ cạnh, góc.
- Đặt \(CD = x\), sử dụng các mối quan hệ ở trên tìm \(x\)
