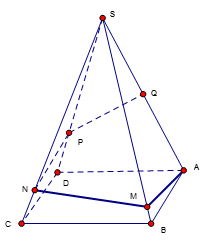
Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D. \(AB = 3a;\,\,AD = DC = a.\) Gọi I là trung điểm của AD, biết hai mặt phẳng (SBI) và (SCI) vuông góc với đáy và mặt phẳng (SBC) tạo với đáy góc \({60^0}\). Tính khoảng cách từ I đến mặt phẳng (SBC).
Trả lời bởi giáo viên
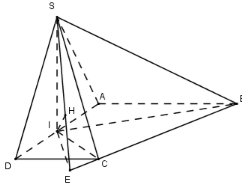
\(\left\{ \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)\)
Trong (ABCD) kẻ \(IE \bot BC\) ta có
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot IE\\BC \bot SI\end{array} \right. \Rightarrow BC \bot \left( {SIE} \right) \Rightarrow BC \bot SE\\\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SE \bot BC\\\left( {ABCD} \right) \supset IE \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBCD} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {IE;SE} \right)} = \widehat {SEI} = {60^0}\end{array}\)
Trong (SIE) kẻ \(IH \bot SE \Rightarrow IH \bot BC \Rightarrow IH \bot \left( {SBC} \right) \Rightarrow d\left( {I;\left( {SBC} \right)} \right) = IH\)
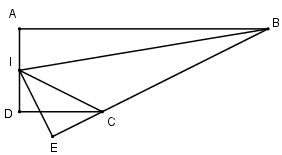
Ta có :
\(\begin{array}{l}{S_{ABI}} = \dfrac{1}{2}AB.AI = \dfrac{1}{2}3a.\dfrac{a}{2} = \dfrac{{3{a^2}}}{4}\\{S_{ICD}} = \dfrac{1}{2}CD.ID = \dfrac{1}{2}a.\dfrac{a}{2} = \dfrac{{{a^2}}}{4}\\{S_{ABCD}} = \dfrac{1}{2}AD\left( {AB + CD} \right) = \dfrac{1}{2}a\left( {a + 3a} \right) = 2{a^2}\\ \Rightarrow {S_{IBC}} = 2{a^2} - \left( {\dfrac{{3{a^2}}}{4} + \dfrac{{{a^2}}}{4}} \right) = {a^2}\end{array}\)
\(BC = \sqrt {{a^2} + {{\left( {2a} \right)}^2}} = a\sqrt 5 \)
Mà \({S_{IBC}} = \dfrac{1}{2}IE.BC \Leftrightarrow IE = \dfrac{{2{S_{IBC}}}}{{BC}} = \dfrac{{2{a^2}}}{{a\sqrt 5 }} = \dfrac{{2a}}{{\sqrt 5 }}\)
Xét tam giác vuông IHE có : \(IH = IE.\sin 60 = \dfrac{{2a}}{{\sqrt 5 }}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt {15} }}{5}\)
Hướng dẫn giải:
+) Mặt mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì giao tuyến của chúng vuông góc với mặt phẳng đó \( \Rightarrow SI \bot \left( {ABCD} \right)\)
+) Xác định góc giữa hai mặt phẳng (ABCD) và (SBC), kẻ \(IE \bot BC,\) chứng minh \(\widehat {\left( {\left( {SBCD} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {IE;SE} \right)}\)
+) Kẻ \(IH \bot SE\), chứng minh \(d\left( {I;\left( {SBC} \right)} \right) = IH\), tính IH.