Câu hỏi:
2 năm trước
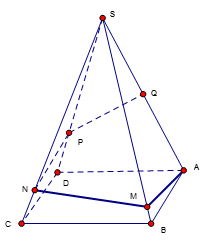
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = 3$,$BC = 4$. Tam giác $SAC$ nằm trong mặt phẳng vuông góc với đáy, khoảng cách từ điểm $C$ đến đường thẳng $SA$ bằng $4$. Côsin của góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAC} \right)$ bằng:
Trả lời bởi giáo viên
Đáp án đúng: b
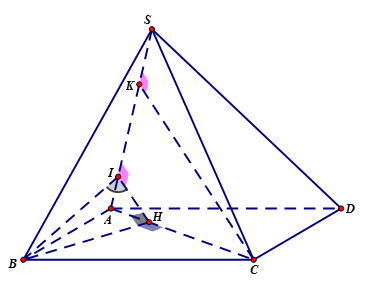
- Dựng \(BH \bot AC\) tại $H$, theo giả thiết suy ra \(BH \bot \left( {SAC} \right)\)\( \Rightarrow BH \bot SA\).
- Dựng \(HI \bot SA\) tại $I$\( \Rightarrow SA \bot \left( {BHI} \right)\)\( \Rightarrow \widehat {BIH}\) là góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAC} \right)$.
- Dựng \(CK \bot SA\) tại $K$ \( \Rightarrow CK = 4\) là khoảng cách từ $C$ đến $SA$.
- Ta có: \(BH = \dfrac{{BA.BC}}{{AC}}\)\( = \dfrac{{3.4}}{5} = \dfrac{{12}}{5}\)\( \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} = \dfrac{9}{5}\).
\(IH{\rm{//}}CK\)\( \Rightarrow \dfrac{{HI}}{{CK}} = \dfrac{{AH}}{{AC}} = \dfrac{9}{{25}}\)\( \Rightarrow HI = \dfrac{9}{{25}}.CK = \dfrac{{36}}{{25}}\)
\( \Rightarrow \tan \widehat {BIH} = \dfrac{{BH}}{{HI}} = \dfrac{5}{3}\)\( \Rightarrow \cos \widehat {BIH} = \dfrac{1}{{\sqrt {1 + {{\tan }^2}\widehat {BIH}} }} = \dfrac{3}{{\sqrt {34} }}\).
Vậy \(\cos \widehat {BIH} = \dfrac{{3\sqrt {34} }}{{34}}\).
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) (góc giữa hai đường thẳng cùng vuông góc với giao tuyến)
- Dựng khoảng cách từ \(C\) đến \(SA\).
- Tính góc giữa hai mặt phẳng bằng cách sử dụng các kiến thức hình học đã biết.
