Câu hỏi:
2 năm trước
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, $SA \bot (ABCD)$, $SA = a\sqrt 3 $. Gọi M là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng AB và CM.
Trả lời bởi giáo viên
Đáp án đúng: b
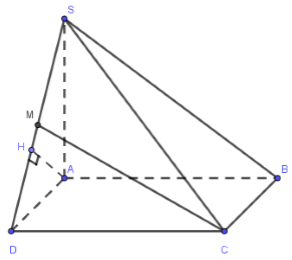
AB // CD$ \Rightarrow AB//(SCD) \supset CM$
$ \Rightarrow d\left( {AB,CM} \right) = d\left( {AB;(SCD)} \right) = d(A,(SCD))$
Kẻ $AH \bot SD,\,\,H \in SD\,\,\left( 1 \right)$ ta có: \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow SD \bot AH\,\,\left( 2 \right)\)
Từ \(\left( 1 \right),\left( 2 \right) \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = AH \Rightarrow d\left( {AB,CM} \right) = AH\).
Tam giác SAD vuông tại A, $AH \bot SD,\,\,H \in SD$, suy ra:
$\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{D^2}}} = \dfrac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{4}{{3{a^2}}} \Rightarrow A{H^2} = \dfrac{{3{a^2}}}{4} \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}$
Vậy khoảng cách giữa 2 đường thẳng CM và AB là $\dfrac{{a\sqrt 3 }}{2}$.
Hướng dẫn giải:
Chuyển từ bài toán tính khoảng cách giữa 2 đường thẳng chéo nhau sang bài toán tính khoảng cách từ điểm đến mặt phẳng
