Câu hỏi:
2 năm trước
Cho hình hộp \(ABCD.A'B'C'D'\). Tìm giá trị của \(k\) thích hợp điền vào đẳng thức véc tơ: \(\overrightarrow {AC} + \overrightarrow {BA'} + k\left( {\overrightarrow {DB} + \overrightarrow {C'D} } \right) = \overrightarrow 0 \).
Trả lời bởi giáo viên
Đáp án đúng: b
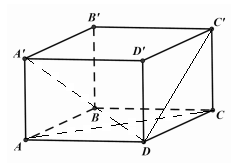
Với \(k = 1\) ta có: \(\overrightarrow {AC} + \overrightarrow {BA'} + 1.\left( {\overrightarrow {DB} + \overrightarrow {C'D} } \right) \) \(= \overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {C'B} \) \(= \overrightarrow {AC} + \overrightarrow {C'A'} = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \)
Hướng dẫn giải:
Thử đáp án, cho các giá trị của \(k\) và kiểm tra thỏa mãn điều kiện đề bài.