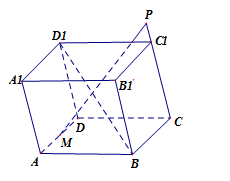
Cho hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\). \(M\) là điểm trên cạnh \(AD\) sao cho \(\overrightarrow {AM}  = \dfrac{1}{3}\overrightarrow {AD} .\) \(N\) là điểm trên đường thẳng \(B{D_1}\). \(P\) là điểm trên đường thẳng \(C{C_1}\) sao cho \(M,N,P\) thẳng hàng.

Tính \(\dfrac{{\left| {\overrightarrow {MN} } \right|}}{{\left| {\overrightarrow {NP} } \right|}}\).

Đặt  $\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {AD}  = \overrightarrow b ,\overrightarrow {A{A_1}}  = \overrightarrow c $  và \(\overrightarrow {BN}  = x\overrightarrow {B{D_1}} ;\overrightarrow {CP}  = y\overrightarrow {C{C_1}}  = y\overrightarrow c \).

Ba điểm \(M,N,P\) thẳng hàng nên \(\overrightarrow {MN}  = \alpha .\overrightarrow {NP} \left( 1 \right)\).

Ta có: \(\overrightarrow {MN}  = \overrightarrow {MA}  + \overrightarrow {AB}  + \overrightarrow {BN} \)

\(\begin{array}{l} =  - \dfrac{1}{3}\overrightarrow b  + \overrightarrow a  + x\overrightarrow {B{D_1}} \\ =  - \dfrac{1}{3}\overrightarrow b  + \overrightarrow a  + x\left( {\overrightarrow {BA}  + \overrightarrow {BC}  + \overrightarrow {B{B_1}} } \right)\\ =  - \dfrac{1}{3}\overrightarrow b  + \overrightarrow a  + x\left( { - \overrightarrow a  + \overrightarrow b  + \overrightarrow c } \right) \\= \left( {1 - x} \right)\overrightarrow a  + \left( {x - \dfrac{1}{3}} \right)\overrightarrow b  + x\overrightarrow c {\rm{ }}\left( 2 \right)\end{array}\)

Ta lại có:

\(\begin{array}{l}\overrightarrow {NP}  = \overrightarrow {NB}  + \overrightarrow {BC}  + \overrightarrow {CP}  \\=  - x\overrightarrow {B{D_1}}  + \overrightarrow b  + y\overrightarrow c  \\=  - x\left( {\overrightarrow b  - \overrightarrow a  + \overrightarrow c } \right) + \overrightarrow b  + y\overrightarrow c \\ \Rightarrow \overrightarrow {NP}  = x\overrightarrow a  + \left( {1 - x} \right)\overrightarrow b  + \left( {y - x} \right)\overrightarrow c {\rm{ }}\left( 3 \right)\end{array}\)

Thay (2), (3) vào (1) ta được:

\(\left\{ \begin{array}{l}1 - x = \alpha x\\x - \dfrac{1}{3} = \alpha \left( {1 - x} \right)\\x = \alpha \left( {y - x} \right)\end{array} \right.\) . Giải hệ ta được \(\alpha  = \dfrac{2}{3},x = \dfrac{3}{5},y = \dfrac{3}{2}\).

Vậy \(\dfrac{{\left| {\overrightarrow {MN} } \right|}}{{\left| {\overrightarrow {NP} } \right|}} = \dfrac{2}{3}\).