Câu hỏi:
2 năm trước
Cho hình lập phương $ABCD.{A_1}{B_1}{C_1}{D_1}$ . Khi đó tổng 3 góc $(\overrightarrow {{D_1}{A_1}} ,\overrightarrow {C{C_1}} ) + (\overrightarrow {{C_1}B} ,\overrightarrow {D{D_1}} ) + (\overrightarrow {D{C_1}} ,\overrightarrow {{A_1}B} )$ là:
Trả lời bởi giáo viên
Đáp án đúng: d
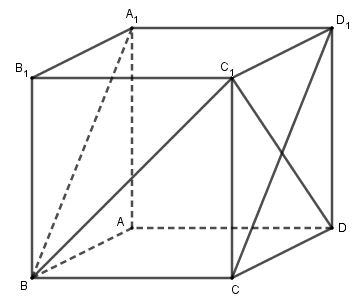
Ta có:
$\begin{array}{l}(\overrightarrow {{D_1}{A_1}} ,\overrightarrow {C{C_1}} ) = {90^0}\\(\overrightarrow {{C_1}B} ,\overrightarrow {D{D_1}} ) = (\overrightarrow {{C_1}B} ,\overrightarrow {C{C_1}} ) = {135^0}\\(\overrightarrow {D{C_1}} ,\overrightarrow {{A_1}B} ) = (\overrightarrow {D{C_1}} ,\overrightarrow {{D_1}C} ) = {90^0}\end{array}$
$ \Rightarrow (\overrightarrow {{D_1}{A_1}} ,\overrightarrow {C{C_1}} ) + (\overrightarrow {{C_1}B} ,\overrightarrow {D{D_1}} ) + (\overrightarrow {D{C_1}} ,\overrightarrow {{A_1}B} ) $ $= {90^0} + {135^0} + {90^0} = {315^0}$
Hướng dẫn giải:
Dựa vào mối quan hệ các véc tơ bằng nhau, tìm góc giữa các véc tơ và tính tổng.
