Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\). Trên các cạnh \(AD,BC\) lần lượt lấy \(M, N\) sao cho $AM = 3MD;{\rm{ }}BN = 3NC$. Gọi \(P,Q\) lần lượt là trung điểm của $AD,BC$. Trong các khẳng định sau, khẳng định nào sai?
Trả lời bởi giáo viên
Đáp án đúng: d
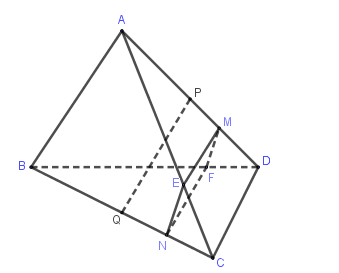
Lấy điểm E trên cạnh AC sao cho AE=3EC, lấy F trên BD sao cho BF=3FD
$\left\{ \begin{array}{l}NE//AB,NE = \dfrac{1}{3}AB\\MF//AB,MF = \dfrac{1}{3}AB\end{array} \right. \Rightarrow NE//MF,NE//MF$
$ \Rightarrow $ NEMF là hình bình hành và 3 vec tơ $\overrightarrow {BA} ,\,\overrightarrow {DC} ,\,\overrightarrow {MN} $ có giá song song hoặc nằm trên mặt phẳng (MFNE) $ \Rightarrow $$\overrightarrow {BA} ,\,\overrightarrow {DC} ,\,\overrightarrow {MN} $ đồng phẳng.
A đúng.
Gọi \(I,K\) lần lượt là trung điểm của \(AC,BD\).
Khi đó \(MN//\left( {PIQK} \right),\) \(DC//\left( {PIQK} \right),\) \(PQ \subset \left( {PIQK} \right)\) nên các véc tơ \(\overrightarrow {MN} ,\overrightarrow {DC} ,\overrightarrow {PQ} \) đồng phẳng.
B đúng.
Ta có: \(AB//\left( {PIQK} \right),\) \(DC//\left( {PIQK} \right),\) \(PQ \subset \left( {PIQK} \right)\) nên các véc tơ \(\overrightarrow {AB} ,\overrightarrow {DC} ,\overrightarrow {PQ} \) đồng phẳng.
C đúng.
Lại có: \(AC,DC \subset \left( {ADC} \right)\) nhưng \(MN \cap \left( {ACD} \right) = M\) nên ba véc tơ \(\overrightarrow {AC} ,\overrightarrow {DC} ,\overrightarrow {MN} \) không có giá song hoặc nằm trên mặt phẳng nào.
Vậy ba véc tơ này không đồng phẳng hay D sai.
Hướng dẫn giải:
Ba véc tơ được gọi là đồng phẳng nếu giá của chúng cùng song song hoặc cùng nằm trên một mặt phẳng.
