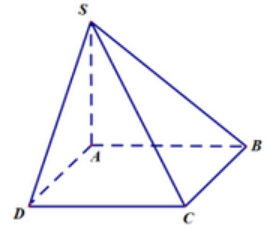
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, $AB = 6;AD = 4;$ $\overrightarrow {AB} .\overrightarrow {AD}  = -12$ . Tính ${\left( {\overrightarrow {SC}  - \overrightarrow {SA} } \right)^2}$

\(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD} \)

\(\overrightarrow {SA}  + \overrightarrow {AB}  = \overrightarrow {SD}  + \overrightarrow {DC} \)

\(\overrightarrow {SA}  + \overrightarrow {AD}  = \overrightarrow {SB}  + \overrightarrow {BC} \).

\(\overrightarrow {SA}  + \overrightarrow {SB}  = \overrightarrow {SC}  + \overrightarrow {SD} \)

\({120^0}\)

\({150^0}\)

\({135^0}\)

\({60^0}\)

$3$.

\( - 6\).

$2$.

\(3\sqrt 3 \).

$\overrightarrow {OG}  = \dfrac{1}{4}(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} )\,\,$

$\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 $

$\overrightarrow {AG}  = \dfrac{2}{3}(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} )$

$\overrightarrow {AG}  = \dfrac{1}{4}(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} )$         

Ba vectơ $\vec x,\,\,\vec y,\,\,\vec z$ đồng phẳng.

Hai vectơ $\vec x,\,\,\vec a$ cùng phương.

Hai vectơ $\vec x,\,\,\vec b$ cùng phương.

Ba vectơ $\vec x,\,\,\vec y,\,\,\vec z$ đôi một cùng phương

$\overrightarrow {A{C_1}}  + \overrightarrow {{A_1}C}  = 2\overrightarrow {AC} $

$\overrightarrow {A{C_1}}  + \overrightarrow {C{A_1}}  + 2\overrightarrow {C_1{C}}  = \overrightarrow 0 $

$\overrightarrow {A{C_1}}  + \overrightarrow {{A_1}C}  = \overrightarrow {A{A_1}} $         

$\overrightarrow {C{A_1}}  + \overrightarrow {AC}  = \overrightarrow {C{C_1}} $

$\overrightarrow {AK}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \dfrac{1}{2}\overrightarrow {A{A_1}} $

$\overrightarrow {AK}  = \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {A{A_1}} $

$\overrightarrow {AK}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {A{A_1}} $

$\overrightarrow {AK}  = \overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {AD}  + \dfrac{1}{2}\overrightarrow {A{A_1}} $