Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD \) và điểm \(G\) thỏa $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 $. Gọi \(O\) là giao điểm của \(GA\) và mặt phẳng \((BCD)\). Trong các khẳng định sau, khẳng định nào đúng?
Trả lời bởi giáo viên
Đáp án đúng: c
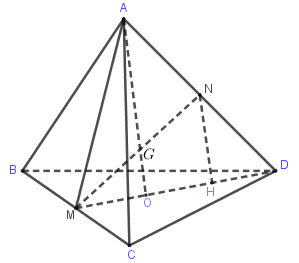
Gọi \(M, N\) là trung điểm của \(BC, AD\)
$ \Rightarrow $ \(G\) là trung điểm \(MN\). Gọi \(H \) là hình chiếu của \(N\) lên \(MD\)
$ \Rightarrow $ NH là đường trung bình của $\Delta AOD$ và \(OG \) là đường trung bình của $\Delta MNH$
$ \Rightarrow OG = \dfrac{1}{2}NH = \dfrac{1}{2}.\dfrac{1}{2}AO$ $ \Rightarrow OG = \dfrac{1}{2}NH = \dfrac{1}{4}.AO$ $ \Rightarrow \overrightarrow {GA} = 3\overrightarrow {OG} $
Hướng dẫn giải:
Nhận xét vị trí của \(G\) dựa vào điều kiện bài cho, từ đó suy ra đáp án đúng.
