Cho hình lập phương $ABCD.{A_1}{B_1}{C_1}{D_1}$ .Gọi \(M\) là trung điểm của \(AD\). Chọn khẳng định đúng:
Trả lời bởi giáo viên
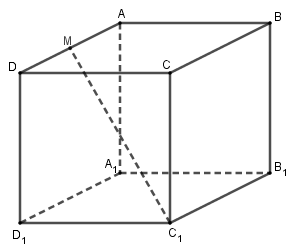
Đáp án A: \(\overrightarrow {{B_1}B} + \overrightarrow {{B_1}A{}_1} + \overrightarrow {{B_1}{C_1}} = \overrightarrow {{B_1}D} \ne \overrightarrow {{B_1}M} \) nên A sai.
Đáp án B: Ta có \(\overrightarrow {{C_1}M} = \overrightarrow {{C_1}{D_1}} + \overrightarrow {{{\rm{D}}_1}{\rm{D}}} + \overrightarrow {DM} = \overrightarrow {{C_1}{D_1}} + \overrightarrow {{C_1}C} + \dfrac{1}{2}\overrightarrow {{C_1}{B_1}} \) nên B đúng và C sai.
Đáp án D: \(\overrightarrow {B{B_1}} + \overrightarrow {{B_1}{A_1}} + \overrightarrow {{B_1}C{}_1} \) \( = \overrightarrow {B{A_1}} + \overrightarrow {{A_1}{D_1}} = \overrightarrow {B{D_1}} \ne 2\overrightarrow {{B_1}D} \) nên D sai.
Hướng dẫn giải:
Xen điểm, sử dụng các quan hệ véc tơ bằng nhau để xét tính đúng sai của từng đáp án.