Câu hỏi:
2 năm trước
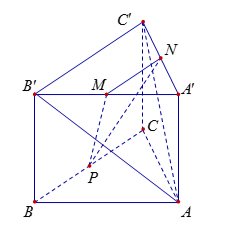
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$, $AB = 6{\rm{cm}}$, $BC = BB' = 2{\rm{cm}}$. Điểm $E$ là trung điểm cạnh $BC$. Một tứ diện đều $MNPQ$ có hai đỉnh $M$ và $N$ nằm trên đường thẳng $C'E$, hai đỉnh $P$, $Q$ nằm trên đường thẳng đi qua điểm $B'$ và cắt đường thẳng $AD$ tại điểm $F$. Khoảng cách $DF$ bằng
Trả lời bởi giáo viên
Đáp án đúng: b
Do tứ diện $MNPQ$ đều nên ta có $MN \bot PQ$ hay $EC' \bot BF$.
Ta có: $\overrightarrow {B'F} = \overrightarrow {B'A} + \overrightarrow {AF} = \overrightarrow {B'A'} + \overrightarrow {B'B} + k\overrightarrow {AD} = \overrightarrow {B'A'} + \overrightarrow {B'B} + k\overrightarrow {B'C'} $
Và $\overrightarrow {EC'} = \overrightarrow {EC} + \overrightarrow {CC'} = \dfrac{1}{2}\overrightarrow {B'C'} - \overrightarrow {B'B} $
Khi đó, $\overrightarrow {EC'} .\overrightarrow {BF} = - B'{B^2} + \dfrac{k}{2}B'{C'^2} = - 4 + \dfrac{k}{2}.4 = 0$$ \Rightarrow k = 2$. Vậy $\overrightarrow {AF} = 2\overrightarrow {AD} $
Vậy $F$ là điểm trên $AD$ sao $D$ là trung điểm của $AF$.
Do đó $DF = BC = 2{\rm{cm}}$.
Hướng dẫn giải:
Sử dụng phương pháp véc tơ và tính chất tứ diện đều (hai cặp cạnh đối vuông góc) tìm vị trí điểm \(F\).
