Câu hỏi:
2 năm trước
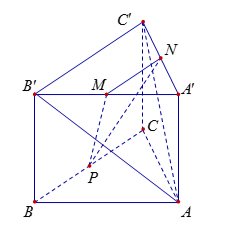
Cho hình hộp \(ABCD.A'B'CD'\)có tất cả các cạnh đều bằng $1$ và các góc phẳng đỉnh \(A\) đều bằng \(60^\circ \). Tính khoảng cách giữa hai đường thẳng \(AB'\) và \(A'C'\)
Trả lời bởi giáo viên
Đáp án đúng: a
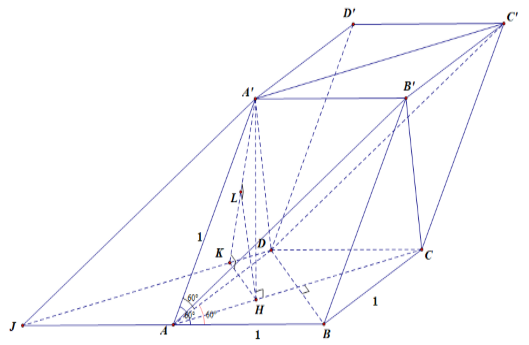
Ta có \(\widehat {BAA'\,} = \widehat {DAA'}\)\( = \widehat {BAD} = 60^\circ \) và \(AB = AD\)\( = AA' = 1\).
Khi đó \(\Delta ABD\), \(\Delta ADA'\) và \(\Delta ABA'\) đều cạnh bằng $1$.
\( \Rightarrow A'D = A'A\)\( = A'B = 1\). Suy ra hình chiếu của \(A'\) lên \(\left( {ABCD} \right)\) là tâm H của \(\Delta ABD\) đều.
Ta có \(AB'\;{\rm{//}}\;DC'\)\( \Rightarrow d\left( {AB';A'C'} \right) = d\left( {AB';\left( {DA'C'} \right)} \right)\)\( = d\left( {H;\left( {DA'C'} \right)} \right)\).
Dựng hình bình hành \(DCAJ\). Từ \(H\) kẻ \(HK \bot DJ\)\(\left( {K \in DJ} \right)\), ta có \(HK\;{\rm{//}}\;DB\).
Từ \(H\) kẻ \(HL \bot A'K\)\(\left( {L \in A'K} \right)\)\( \Rightarrow HL \bot \left( {DA'C'} \right)\)\( \Rightarrow d\left( {H;\left( {DA'C'} \right)} \right) = HL\).
Ta có: \(HK = \dfrac{1}{2}\), \(A'H = \sqrt {1 - {{\left( {\dfrac{{\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{\sqrt 6 }}{3}\).
Xét tam giác \(A'HK\): \(\dfrac{1}{{H{L^2}}} = \dfrac{1}{{H{K^2}}} + \dfrac{1}{{A'{H^2}}}\)\( \Rightarrow HL = \dfrac{{\sqrt {22} }}{{11}}\).
Hướng dẫn giải:
- Sử dụng lý thuyết: \(d\left( {a,b} \right) = d\left( {a,\left( P \right)} \right) = d\left( {A,\left( P \right)} \right) = AH\), ở đó \(a,b\) chéo nhau, \(a//\left( P \right) \supset b\), \(A \in a,\) \(H\) là hình chiếu của \(A\) lên \(\left( P \right)\)
