Câu hỏi:
2 năm trước
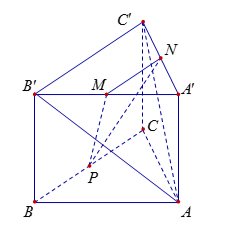
Cho hình lập phương ABCD có cạnh là 2. Gọi M, N lần lượt là trung điểm của BC và CD. Tính diện tích thiết diện của hình lập phương khi cắt bởi mặt phẳng (A’MN).
Trả lời bởi giáo viên
Đáp án đúng: a
Kéo dài MN cắt AB và AD lần lượt tại E và F.
Gọi \(H = A'E \cap BB';\,\,K = A'F \cap DD'\). Khi đó thiết diện là A’HMNK.
Ta có ABMND là hình chiếu của A’HMNK trên mặt phẳng \(\left( {ABCD} \right)\).
Gọi \(I = AC \cap MN\) ta có: \(AC \bot BD;\,\,MN//BD \Rightarrow AC \bot MN\) tại I.
\(\left\{ \begin{array}{l}MN \bot AI\\MN \bot AA'\end{array} \right. \Rightarrow MN \bot \left( {A'AI} \right) \Rightarrow MN \bot A'I\)
\( \Rightarrow \widehat {\left( {\left( {A'HMNK} \right);\left( {ABCD} \right)} \right)} = \widehat {AIA'}\)
Ta có :
\(CM = CN = 1 \Rightarrow MN = \sqrt 2 \Rightarrow IC = \dfrac{{\sqrt 2 }}{2}\)
\(AC = 2\sqrt 2 \Rightarrow AI = 2\sqrt 2 - \dfrac{{\sqrt 2 }}{2} = \dfrac{{3\sqrt 2 }}{2}\).
Xét tam giác vuông AA’I có: \(A'I = \sqrt {AA{'^2} + A{I^2}} = \sqrt {4 + \dfrac{9}{2}} = \dfrac{{\sqrt {34} }}{2}\).
\( \Rightarrow \cos \widehat {AIA'} = \dfrac{{AI}}{{A'I}} = \dfrac{{\dfrac{{3\sqrt 2 }}{2}}}{{\dfrac{{\sqrt {34} }}{2}}} = \dfrac{3}{{\sqrt {17} }} = \cos \widehat {\left( {\left( {ABCD} \right);\left( {A'HMNK} \right)} \right)}\)
Ta có \({S_{ABCD}} = 4;\,\,{S_{CMN}}\dfrac{1}{2}.1.1 = \dfrac{1}{2} \Rightarrow {S_{ABMND}} = 4 - \dfrac{1}{2} = \dfrac{7}{2}\)
$ \Rightarrow {S_{A'HMNK}} = \dfrac{{{S_{ABMND}}}}{{\cos \widehat {AIA'}}} = \dfrac{7}{2}.\dfrac{{\sqrt {17} }}{3} = \dfrac{{7\sqrt {17} }}{6}$ .
Hướng dẫn giải:
${S_{A'HMNK}} = \dfrac{{{S_{ABMND}}}}{{\cos \widehat {AIA'}}}$
