Câu hỏi:
3 năm trước
Cho hình chóp S. ABC có đáy là tam giác ABC vuông cân tại A, cạnh SA vuông góc với mặt phẳng đáy, \(SA = \dfrac{{a\sqrt 6 }}{2},AB = a\). Gọi \(M\) là trung điểm của BC. Góc giữa đường thẳng SM và mặt phẳng \((ABC)\) có số đo bằng
Trả lời bởi giáo viên
Đáp án đúng: c
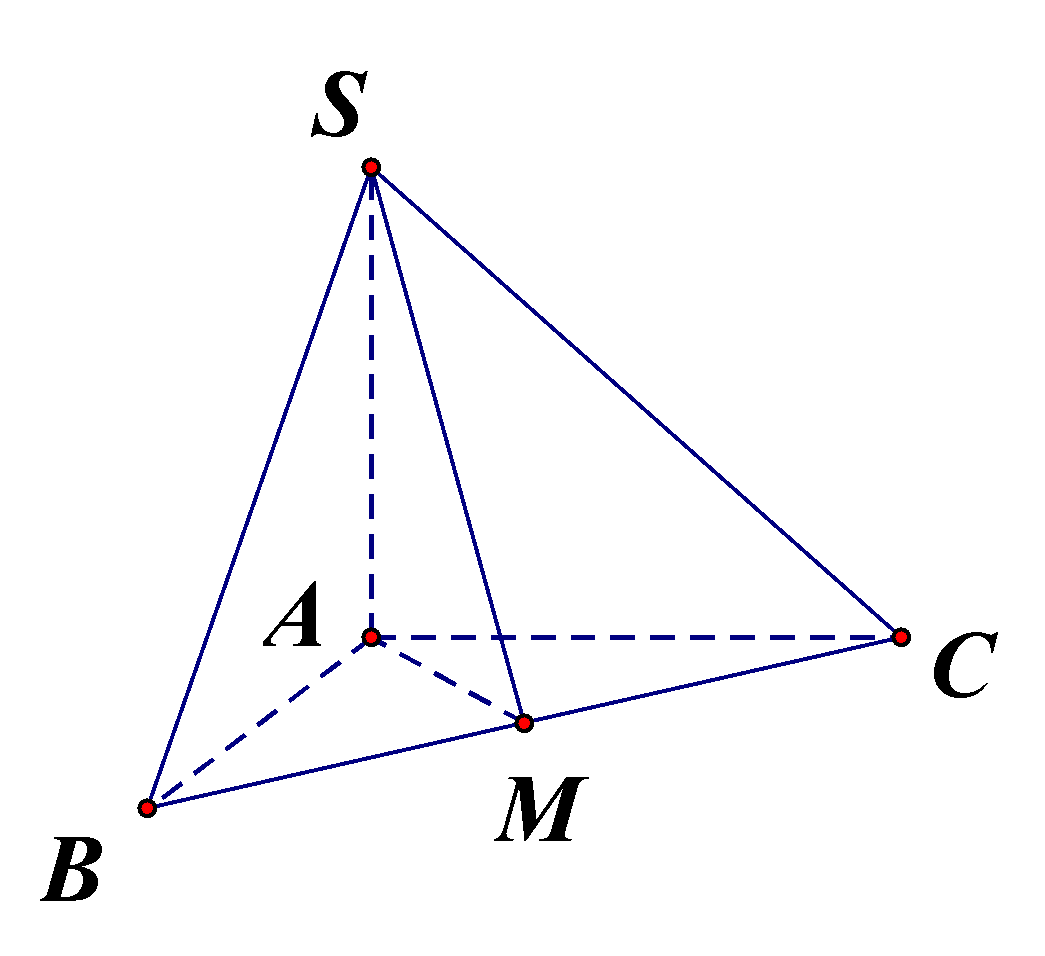
Bước 1: Xác định góc giữa SM và (ABC)
Do SM có hình chiếu vuông góc lên (ABC) là AM.
Do đó \(\widehat {\left( {SM,(ABC)} \right)} = \widehat {SMA}\).
Bước 2: Tính \(\widehat {SMA}\)
Ta có \(AM = \dfrac{{BC}}{2} = \dfrac{{a\sqrt 2 }}{2}\).
Xét tam giác vuông SAM có
\(\tan \widehat {SMA} = \dfrac{{SA}}{{AM}} = \dfrac{{\dfrac{{a\sqrt 6 }}{2}}}{{\dfrac{{a\sqrt 2 }}{2}}} = \sqrt 3 \)\( \Rightarrow \widehat {SMA} = {60^0}\)
Hướng dẫn giải:
Bước 1: Xác định góc giữa SM và (ABC)
Bước 2: Tính \(\widehat {SMA}\)

