Câu hỏi:
3 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật có cạnh \(AB = a\), \(BC = 2a\), cạnh bên \(SA\) vuông góc với đáy, \(SA = a\sqrt {15} \). Tính góc tạo bởi đường thẳng \(SC\) và mặt phẳng \(\left( {ABD} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: c
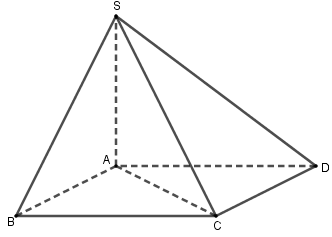
Do \(SA \bot \left( {ABCD} \right)\) nên \(\widehat {SC,\left( {ABD} \right)} = \widehat {SC,\left( {ABCD} \right)} = \widehat {SC,AC} = \widehat {SCA}\)
Xét tam giác vuông \(SAC\), ta có \(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{SA}}{{\sqrt {A{B^2} + B{C^2}} }} = \sqrt 3 \).
Suy ra \(\widehat {SCA} = {60^0}\).
Hướng dẫn giải:
Xác định góc giữa đường thẳng và mặt phẳng (khác \({90^0}\)) là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.

