Cho lăng trụ \(ABCD.A'B'C'D'\) có đáy là hình thoi cạnh \(a\), \(\widehat {BAD} = {60^0}\). Hình chiếu vuông góc của \(B'\) xuống mặt đáy trùng với giao điểm hai đường chéo của đáy và cạnh bên \(BB' = a\). Tính góc giữa cạnh bên và mặt đáy.
Trả lời bởi giáo viên
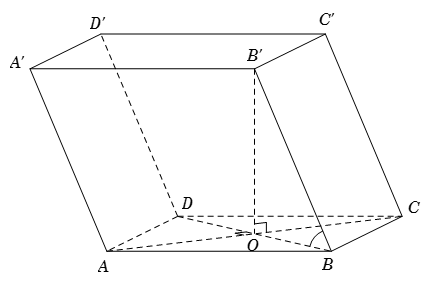
Gọi \(O = AC \cap BD\). Theo giả thiết \(B'O \bot \left( {ABCD} \right)\).
Do đó \(\widehat {BB',\left( {ABCD} \right)} = \widehat {BB',BO} = \widehat {B'BO}\).
Từ giả thiết suy ra tam giác \(ABD\) đều cạnh \(a\), suy ra \(BO = \dfrac{1}{2}BD = \dfrac{a}{2}\).
Tam giác vuông \(B'BO\), có \(\cos \widehat {B'BO} = \dfrac{{BO}}{{BB'}} = \dfrac{1}{2} \Rightarrow \widehat {B'BO} = {60^0}\).
Hướng dẫn giải:
Xác định góc giữa đường thẳng và mặt phẳng (khác \({90^0}\)): là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng

