Câu hỏi:
2 năm trước
Cho lăng trụ \(ABC.A'B'C'\) có các mặt bên là hình vuông cạnh \(a\). Gọi \(D\), \(E\) lần lượt là trung điểm các cạnh \(BC\), \(A'C'\). Tính khoảng cách giữa đường thẳng \(DE\) và mặt phẳng \(\left( {ABB'A'} \right)\) theo \(a\).
Trả lời bởi giáo viên
Đáp án đúng: b
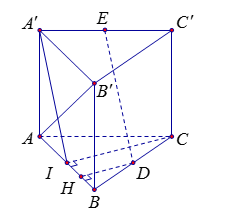
Gọi \(I\) là trung điểm của \(AB\). Khi đó \(CI = \dfrac{{a\sqrt 3 }}{2},\)\(CI \bot \left( {ABB'A'} \right)\)
Gọi \(H\) là trung điểm của \(IB\).
Vì \(DH{\rm{//}}CI\) nên \(DH \bot \left( {ABB'A'} \right)\)
Vì $\left\{ \begin{array}{l}ID{\rm{//}}AC{\rm{//}}A'E\\ID = \dfrac{1}{2}AC = A'E\end{array} \right.$ nên tứ giác \(A'EDI\) là hình bình hành, suy ra $DE\;{\rm{//}}\;A'I \subset \left( {ABB'A'} \right)$.
Ta có $DE\;{\rm{//}}\;\left( {ABB'A'} \right)$.
Vậy \(d\left( {DE,\left( {ABB'A'} \right)} \right) = d\left( {D,\left( {ABB'A'} \right)} \right) = DH = \dfrac{{CI}}{2} = \dfrac{{a\sqrt 3 }}{4}\)
Hướng dẫn giải:
Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm thuộc đường thẳng này đến mặt phẳng kia.
