Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\) cạnh \(a\), \(SO\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SO = a.\) Khoảng cách giữa đường thẳng \(AB\) và mặt phẳng \(\left( {SCD} \right)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
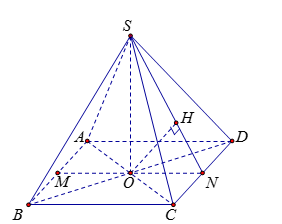
Gọi \(M,N\) lần lượt là trung điểm của các cạnh$AB,CD$; $H$ là hình chiếu vuông góc của \(O\) trên \(SN.\)
Vì $AB{\rm{//}}CD$ nên \(d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)\) (vì \(O\) là trung điểm đoạn \(MN\))
Ta có $\left\{ \begin{array}{l}CD \bot SO\\CD \bot ON\end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH$
Khi đó $\left\{ \begin{array}{l}CD \bot OH\\OH \bot SN\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.$
Tam giác \(SON\) vuông tại \(O\) nên $\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{N^2}}} + \dfrac{1}{{O{S^2}}} = \dfrac{1}{{\dfrac{{{a^2}}}{4}}} + \dfrac{1}{{{a^2}}} = \dfrac{5}{{{a^2}}} \Rightarrow OH = \dfrac{a}{{\sqrt 5 }}$
Vậy \(d\left( {AB,\left( {SCD} \right)} \right) = 2OH = \dfrac{{2a\sqrt 5 }}{5}\).
Hướng dẫn giải:
Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm thuộc mặt phẳng này đến mặt phẳng kia.
