Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B,{\rm{ }}AB = 3a,{\rm{ }}BC = 4a.\) Cạnh bên \(SA\) vuông góc với đáy. Góc tạo bởi giữa \(SC\) và đáy bằng \(60^\circ \). Gọi \(M\) là trung điểm của \(AC\), \(N\) là trung điểm của \(BC\). Tính khoảng cách giữa đường thẳng \(AB\) và mặt phẳng \(\left( {SMN} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: b
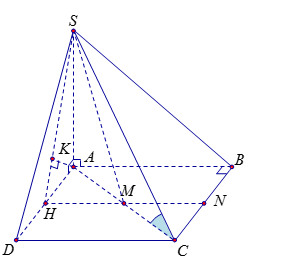
\(AC = 5a,{\rm{ }}SA = 5a\sqrt 3 \).
Ta có: \(AB{\rm{//}}\left( {SMN} \right) \Rightarrow d\left( {AB,\left( {SMN} \right)} \right) = d\left( {A,\left( {SMN} \right)} \right)\).
Dựng \(AH \bot MN\) tại \(H\) trong \(\left( {ABC} \right)\).
Dựng \(AK \bot SH\) tại \(K\) trong \(\left( {{\rm{S}}AH} \right)\).
\( \Rightarrow AK \bot \left( {SMN} \right)\) tại \(K\) nên \(d\left( {A,\left( {SMN} \right)} \right) = AK\)$ \Rightarrow d\left( {AB,\left( {SMN} \right)} \right) = AK$.
\(AH = NB = 2a\).
\(\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{S{A^2}}} = \dfrac{1}{{4{a^2}}} + \dfrac{1}{{75{a^2}}} = \dfrac{{79}}{{300{a^2}}}\) \( \Rightarrow AK = \dfrac{{10a\sqrt 3 }}{{\sqrt {79} }}\).
Hướng dẫn giải:
Khoảng cách giữa đường thẳng song song với mặt phẳng bằng khoảng cách từ một điểm thuộc đường thẳng này đến mặt phẳng kia.
