Câu hỏi:
2 năm trước
Cho lăng trụ đứng tam giác \(ABC.A'B'C'\) có đáy là một tam giác vuông cân tại \(B\), \(AB = BC = a\), \(AA' = a\sqrt 2 \), \(M,E\) là trung điểm \(BC,BB'\). Tính khoảng cách giữa đường thẳng \(B'C\) và mặt phẳng \(\left( {AME} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: a
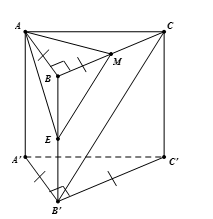
Ta có: $EM{\kern 1pt} \;{\rm{//}}\;B'C$\( \Rightarrow B'C{\kern 1pt} \;{\rm{//}}\;(AME)\)
\( \Rightarrow d\left( {B'C,\left( {AME} \right)} \right) = d\left( {C,\left( {AME} \right)} \right) = d\left( {B,\left( {AME} \right)} \right)\)
Xét khối chóp \(BAME\) có các cạnh \(BE\), \(AB\), \(BM\) đôi một vuông góc với nhau nên
\(\dfrac{1}{{{d^2}\left( {B,\left( {AME} \right)} \right)}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{M{B^2}}} + \dfrac{1}{{E{B^2}}}\)\( \Leftrightarrow \dfrac{1}{{{d^2}\left( {B,\left( {AME} \right)} \right)}} = \dfrac{7}{{{a^2}}}\)\( \Leftrightarrow {d^2}\left( {B,\left( {AME} \right)} \right) = \dfrac{{{a^2}}}{7}\)
\( \Leftrightarrow d\left( {B,\left( {AME} \right)} \right) = \dfrac{a}{{\sqrt 7 }}\).
Hướng dẫn giải:
Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm thuộc đường thẳng này đến mặt phẳng kia.
