Câu hỏi:
3 năm trước
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA\) vuông góc với đáy, \(SA = a\). Khoảng cách giữa đường thẳng \(CD\) và mặt phẳng \(\left( {SAB} \right)\) là
Trả lời bởi giáo viên
Đáp án đúng: a
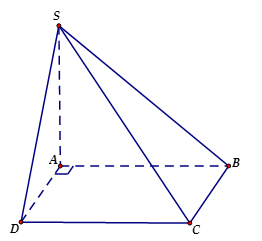
Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AD\).
Ta có: $\left\{ \begin{array}{l}SA \bot AD\\AB \bot AD\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right)$$ \Rightarrow d\left( {D,\,\left( {SAB} \right)} \right) = DA$.
Vì \(CD//AB \subset \left( {SAB} \right)\) nên $d\left( {CD,\,\left( {SAB} \right)} \right)$$ = d\left( {D,\,\left( {SAB} \right)} \right) = DA = a$
Hướng dẫn giải:
Khoảng cách giữa đường thẳng song song với mặt phẳng bằng khoảng cách từ một điểm thuộc đường thẳng này đến mặt phẳng kia.

