Câu hỏi:
2 năm trước
Cho hình lập phương ABCD. A’B’C’D’ có tất cả các cạnh bằng 2. Khoảng cách giữa hai mặt phẳng (AB’D’) và (BC’D) bằng:
Trả lời bởi giáo viên
Đáp án đúng: b
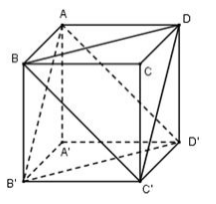
Dễ thấy BD // B’D’, BC’ // AD’ nên (AB’D’) // (BC’D)
$ \Rightarrow d\left( {\left( {AB'D'} \right);\left( {BC'D} \right)} \right) = d\left( {C';\left( {AB'D'} \right)} \right) = \dfrac{{3{V_{C'.AB'D'}}}}{{{S_{AB'D'}}}}$
Ta có :
$\begin{array}{l}{V_{C'.AB'D'}} = {V_{A.B'C'D'}} = \dfrac{1}{3}AA'.{S_{B'C'D'}} = \dfrac{1}{3}AA'.\dfrac{1}{2}B'C'.C'D'\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \dfrac{1}{6}{V_{ABCD.A'B'C'D'}} = \dfrac{1}{6}{.2^3} = \dfrac{4}{3}\end{array}$
Tam giác AB’D’ có $AB' = AD' = B'D' = 2\sqrt 2 \Rightarrow \Delta AB'D'$ là tam giác đều cạnh
$2\sqrt 2 \Rightarrow {S_{AB'D'}} = \dfrac{{{{\left( {2\sqrt 2 } \right)}^2}\sqrt 3 }}{4} = 2\sqrt 3 $
Vậy $d\left( {C';\left( {AB'D'} \right)} \right) = \dfrac{{3.\dfrac{4}{3}}}{{2\sqrt 3 }} = \dfrac{2}{{\sqrt 3 }} \Rightarrow d\left( {\left( {AB'D'} \right);\left( {BC'D} \right)} \right) = \dfrac{2}{{\sqrt 3 }}$.
Hướng dẫn giải:
Tính khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ 1 điểm bất kì trên mặt phẳng này đến mặt phẳng kia.
